广西南宁市西乡塘区2024年九年级下学期中考数学二模试卷

更新时间：2024-08-23 浏览次数：17 类型：中考模拟

一、选择题（共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑。）

1. (2024九下·东营模拟) 2024的绝对值是（）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·南宁模拟) 如图， $\text{[math]}$ ，要使 $\text{[math]}$ ，则 $\text{[math]}$ 的大小是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·南宁模拟) 如图是一个几何体的主视图，则该几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024·南宁模拟) 2024年广西三月三假期（4月11日至14日），南宁市文化旅游活动丰富多彩，旅游接待总人数和旅游总收入实现“双增长”，其中，南宁“三街两巷”累计接待市民游客660000人次．数据“660000”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·南宁模拟) 欣欣想在自己房间的墙上钉一个直线型饰品挂架，用来挂自己喜欢的装饰物，为了固定饰品挂架，欣欣至少需要钉子（）

A . 1根 B . 2根 C . 3根 D . 4根

答案解析收藏纠错 + 选题
6. (2024·南宁模拟) 一个不等式组的解集在数轴上表示如图，则这个不等式组的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
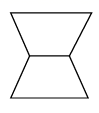
7. (2024·南宁模拟) 一个小球在如图所示的地板上自由滚动，并随机停在某块方砖上．如果每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·南宁模拟) 如果式子 $\text{[math]}$ 有意义，那么a的值可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
9. (2024·南宁模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的半径， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·南宁模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024·南宁模拟) 2024年汤姆斯杯羽毛球赛于4月27日至5月5日在成都举行，根据赛制规定，所有参赛队伍先通过抽签分成若干小组进行小组赛，小组赛阶段每队都要与小组内其他队进行一场比赛，已知中国队所在的小组有n支队伍，共安排了6场小组赛．根据题意，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024·南宁模拟) 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的顶点A在x轴负半轴上，顶点B在x轴正半轴上．若抛物线 $\text{[math]}$ 经过点C ， D ，则点B的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分．）

13. (2024·南宁模拟) 比较大小：0 $\text{[math]}$ （填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）．

答案解析收藏纠错 + 选题
14. (2024·上虞模拟) 分解因式： $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2024·南宁模拟) 为了了解某市10000名中学生的睡眠时间情况，在该市范围内随机抽取500名学生进行调查，这次抽样调查的样本容量是．

答案解析收藏纠错 + 选题
16. (2024·南宁模拟) 在平面直角坐标系中，点 $\text{[math]}$ 与点B关于y轴对称，则点B的坐标是．

答案解析收藏纠错 + 选题
17. (2024·南宁模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，任取一点O ，使点O和点A在直线 $\text{[math]}$ 的两侧，以点A为圆心， $\text{[math]}$ 长为半径作弧，交 $\text{[math]}$ 于点M ， N ，分别以点M ， N为圆心，大于 $\text{[math]}$ 长为半径作弧，两弧相交于点P ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点D ．若 $\text{[math]}$ 的长为3，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
18. (2024·南宁模拟) 如图，将边长 $\text{[math]}$ ， $\text{[math]}$ 的矩形 $\text{[math]}$ 沿对角线 $\text{[math]}$ 剪开，得到 $\text{[math]}$ 和 $\text{[math]}$ ，将 $\text{[math]}$ 沿射线 $\text{[math]}$ 方向平移，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，当 $\text{[math]}$ 时，平移距离 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤．）

19. (2024·南宁模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024·南宁模拟) 解方程组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024·南宁模拟) 如图，在边长均为1个单位长度的小正方形网格中， $\text{[math]}$ 的顶点均在格点（网格线的交点）上．
1. （1）将 $\text{[math]}$ 向右平移4个单位长度得到的 $\text{[math]}$ ，请画出 $\text{[math]}$ ；
2. （2）若点C的坐标为 $\text{[math]}$ ，请你在网格中画出平面直角坐标系 $\text{[math]}$ ，点O为坐标原点；
3. （3）在（2）的条件下，请画出 $\text{[math]}$ 关于点O对称的图形 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
22. (2024·南宁模拟) 四月份广西的西瓜已经上市，为了了解“麒麟”和“美都”两种西瓜的品质（大小、甜度等），进行了抽样调查，在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集，整理，下面是两种西瓜得分的统计表．
两种西瓜得分表
样品序号
1
2
3
4
5
6
7
麒麟
76
85
86
89
90
95
95
美都
81
84
87
87
90
93
94
两种西瓜得分统计表
统计量
平均数
中位数
众数
麒麟
88
a
95
美都
88
87
b
两种西瓜得分折线统计图
根据以上信息，解答下列问题：
1. （1）上述统计表中 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）从折线统计图看，两种西瓜得分的方差 $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）；
3. （3）请从平均数，方差，中位数，众数这四个统计量中选择合适的量，评判这两种样品瓜哪种品质较好，并说明理由．
答案解析收藏纠错 + 选题
23. (2024·南宁模拟) 在日常生活中，当手机剩余电量为 $\text{[math]}$ 时，张老师便会给手机充电，他发现单独使用快充充电器和单独用普通充电器对该手机充电，手机电量y（单位： $\text{[math]}$ ）与充电时间x（单位：分钟）的函数图象分别为图中的线段 $\text{[math]}$ ， $\text{[math]}$ ．请根据图中信息，解答下列问题：
1. （1）张老师单独用快充充电器充满电比用普通充电器少用分钟；
2. （2）求线段 $\text{[math]}$ 对应的函数表达式（不要求写出自变量的取值范围）；
3. （3）张老师若先用普通充电器充电m分钟后，再改用快充充电器直至充满，共用70分钟，请求出m的值．
答案解析收藏纠错 + 选题
24. (2024·南宁模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 和 $\text{[math]}$ 分别是 $\text{[math]}$ 的切线， $\text{[math]}$ 平分 $\text{[math]}$ ，且与 $\text{[math]}$ 交于点E ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2024·南宁模拟) 为巩固扶贫攻坚成果，促进农民收入持续增长，某县政府鼓励农民结合本地实际开发特色农作物种植．经了解，某农户近五年种植该农作物的年收入如表所示：
第x年
1
2
3
4
5
年收入y（万元）
1.5
2.5
4.5
7.5
11.3
在直角坐标系中用点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 表示近五年该农户种植年收入的变化情况．如图所示，拟用下列三个函数之一模拟该农户的种植年收入变化趋势： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以便估算该农户第6年的种植年收入．
1. （1）小明同学认为不能选 $\text{[math]}$ ，你认同吗？请说明理由；
2. （2）你认为选哪个函数最合理，并求出函数表达式；
3. （3）该农户准备在第6年年底购买一台价值16万元的农机设备，根据（2）中你选择的函数表达式，预测该农户第6年的种植年收入能否满足购买农机设备的资金需求．
答案解析收藏纠错 + 选题
26. (2024·南宁模拟) 综合与实践
【问题情境】在综合与实践课上，老师出示了这样一个情境：
在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转得到 $\text{[math]}$ ，点D ， E的对应点分别是点B ， C ．
1. （1）【初探感知】如图1， $\text{[math]}$ $\text{[math]}$ ；
2. （2）【深入领悟】如图2，当线段 $\text{[math]}$ 经过点C时，求证： $\text{[math]}$ ；
3. （3）【融会贯通】如图3，在旋转的过程中，当点D落在 $\text{[math]}$ 的延长线上时，过点E作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点G ．请你判断线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由．
答案解析收藏纠错 + 选题