一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
-
4.
(2024高三下·江西模拟)
某中学举办了一次知识竞赛,从中随机抽取了部分学生的成绩绘制出如图所示的频率分布直方图,则估计该中学本次竞赛成绩的中位数为( )

A . 68
B . 71
C . 75
D . 79
-
A . 8
B . 9
C . 14
D . 15
-
6.
(2024高三下·江西模拟)
某校羽毛球队的4名男生和4名女生分成四组,参加四场混合双打比赛(每名队员只限参加一场比赛),则组队方法的总数为( )
A . 24
B . 288
C . 576
D . 1152
-
7.
(2024高三下·江西模拟)
已知

,

分别是双曲线

(

,
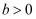
)的左、右焦点,过

的直线交双曲线左支于
A ,
B两点,

,

, 则双曲线
C的渐近线方程为( )
-
8.
(2024高三下·江西模拟)
在学习完“错位相减法”后,善于观察的同学发现对于“等差

等比数列”此类数列求和,也可以使用“裂项相消法”求解.例如

, 故数列

的前
n项和

. 记数列

的前
n项和为

, 利用上述方法求

( )
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
A . z为纯虚数
B .  C .
C .  D . 复数
D . 复数 在复平面内对应的点在第三象限
在复平面内对应的点在第三象限
-
A . 与AB共面且与 共面的棱有5条
B .
共面的棱有5条
B .  C .
C .  的最小值为
的最小值为 D . 若
D . 若 与平面ABCD交于点E , 则
与平面ABCD交于点E , 则 的面积为2
的面积为2
-
三、填空题:本题共3小题,每小题5分,共15分.把答案填在答题卡中的横线上.
-
-
13.
(2024高三下·江西模拟)
已知
A ,
B分别为椭圆

的上、下顶点,
F是椭圆
C的上焦点,

为椭圆
C上一点,若

, 则椭圆
C的离心率为
,椭圆
C的方程为
.
-
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15.
(2024高三下·江西模拟)
为了解人们对环保的认知程度,某市为不同年龄和不同职业的人举办了一次环保知识竞赛,满分100分.随机抽取的8人的得分为84,78,81,84,85,84,85,91.
-
(1)
计算样本平均数

和样本方差

;
-
(2)
若这次环保知识竞赛的得分
X服从正态分布

, 其中

和

的估计值分别为样本平均数

和样本方差

, 若按照

,

,

,

的比例将参赛者的竞赛成绩从低分到高分依次划分为参与奖、二等奖、一等奖、特等奖四个等级,试确定各等级的分数线.(结果保留两位小数)(参考数据:

)
附:若随机变量X服从正态分布 , 则
, 则 ,
,  ,
,  .
.
-
-
(1)
若

, 证明:

平面
DEA .
-
(2)
若
ABC为正三角形,
D是
BC的中点,求二面角

的余弦值.
-
-
-
(2)
若
C为钝角,求

的取值范围.
-
-
(1)
若
Q为圆

上一动点,求

的最小值;
-
(2)
过点
P作圆

的两条切线,分别交抛物线

于
A ,
B两点,切点分别为
E ,
F , 若四边形
ABFE为梯形,求点
P的坐标.
-
-
-
(2)
求

的单调区间;
-

, 则
,
,
.