浙江省湖州市2023-2024学年高一下学期6月期末调研测试...

更新时间：2024-07-23 浏览次数：16 类型：期末考试

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2024高一下·湖州期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 是两个单位向量，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·湖州期末) 已知复数 $\text{[math]}$ 满足 $\text{[math]}$ （ $\text{[math]}$ 为虚数单位），则 $\text{[math]}$ 在复平面内对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024高一下·湖州期末) 已知圆锥的母线长为 $\text{[math]}$ ，其侧面展开图为一个半圆，则该圆锥的底面半径是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一下·宜春期末) 设 $\text{[math]}$ ， $\text{[math]}$ 是两个平面，m ， n是两条直线，则下列命题为真命题的是（）

A . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·湖州期末) 如图所示的频率分布直方图呈现右拖尾形态，则根据此图作出以下判断，正确的是（）

A . 众数<中位数<平均数 B . 众数<平均数<中位数 C . 中位数<平均数<众数 D . 中位数<众数<平均数

答案解析收藏纠错 + 选题
6. (2024高一下·湖州期末) 在正方体 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的中点，则异面直线DE与AC所成角的余弦值是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·湖州期末) 湖州东吴国际双子大厦是湖州目前已建成的第一高楼，也被称为浙北第一高楼，是湖州的一个壮观地标．如图，为测量双子大厦的高度CD ，某人在大厦的正东方向找到了另一建筑物，其高AB约192m，在它们之间的地面上的点M（B ， M ， D共线）处测得建筑物顶A、大厦顶C的仰角分别为45°和60°，在建筑物顶A处测得大厦顶C的仰角为15°，则可估算出双子大厦的高度CD约为（）

A . 284m B . 286m C . 288m D . 290m

答案解析收藏纠错 + 选题
8. (2024高一下·湖州期末) 已知 $\text{[math]}$ 是锐角三角形，若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. (2024高一下·湖州期末) 为了丰富同学们的课外活动，某学校为同学们举办了四种不同的科普活动：科技展览、科普讲座、科技游艺、科技绘画．记事件A：只参加科技游艺活动；事件B：至少参加两种科普活动；事件C：只参加一种科普活动；事件D：一种科普活动都不参加；事件E：至多参加一种科普活动，则下列说法正确的是（）

A . A与D是互斥事件 B . B与E是对立事件 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一下·湖州期末) 若复数z ， w均不为0，则下列结论正确的是*

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一下·湖州期末) 如图，一张矩形白纸 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， E ， F分别为AD ， BC的中点，BE交AC于点M ， DF交AC于点 $\text{[math]}$ ．现分别将 $\text{[math]}$ ， $\text{[math]}$ 沿BE ， DF折起，且点A ， C在平面 $\text{[math]}$ 的同侧，则下列命题正确的是（）

A . 当平面 $\text{[math]}$ 平面 $\text{[math]}$ 时， $\text{[math]}$ 平面 $\text{[math]}$ B . 当A ， C重合于点 $\text{[math]}$ 时， $\text{[math]}$ 平面 $\text{[math]}$ C . 当A ， C重合于点 $\text{[math]}$ 时，三棱锥 $\text{[math]}$ 的外接球的表面积为 $\text{[math]}$ D . 当A ， C重合于点 $\text{[math]}$ 时，四棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分．

12. (2024高一下·湖州期末) 已知事件 $\text{[math]}$ 和事件 $\text{[math]}$ 相互独立，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024高一下·湖州期末) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 在 $\text{[math]}$ 上的投影向量的坐标是．

答案解析收藏纠错 + 选题
14. (2024高一下·湖州期末) 已知四面体 $\text{[math]}$ 中，棱BC ， AD所在直线所成的角为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则四面体 $\text{[math]}$ 体积的最大值是．

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤．

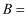
15. (2024高一下·湖州期末) 若某袋中有5个大小质地完全相同的球，其中2个红球、3个黄球从中不放回地依次随机摸出2个球，记事件 $\text{[math]}$ “第一次摸到红球”，事件 $\text{[math]}$ “第二次摸到红球”．
1. （1）求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
2. （2）求两次摸到的不都是红球的概率．
答案解析收藏纠错 + 选题
16. (2024高二下·长沙期末) 在 $\text{[math]}$ 中，角A ， B ， C的对边分别为a ， b ， c ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 边上的高为1，求 $\text{[math]}$ 的周长．
答案解析收藏纠错 + 选题
17. (2024高一下·湖州期末) 某学校组织“防电信诈骗知识”测试，随机调查400名学生，将他们的测试成绩（满分100分）的统计结果按 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 依次分成第一组至第五组，得到如图所示的频率分布直方图．
1. （1）求图中x的值；
2. （2）估计参与这次测试学生的成绩的平均数（同一组中的数据用该组区间的中点值为代表）和第60百分位数；
3. （3）现从以上第三组、第四组和第五组中参与测试的学生用分层随机抽样的方法选取15人，担任学校“防电信诈骗知识”的宣传员．若这15名学校宣传员中来自第三组学生的测试成绩的平均数和方差分别为75和5，来自第四组学生的测试成绩的平均数和方差分别为85和10，来自第五组学生的测试成绩的平均数和方差分别为93和5.2，据此估计这次第三组、第四组和第五组所有参与测试学生的成绩的方差．
答案解析收藏纠错 + 选题
18. (2024高一下·广东期末) 如图，在四棱台 $\text{[math]}$ 中，底面 $\text{[math]}$ 为菱形，且 $\text{[math]}$ ， $\text{[math]}$ ，侧棱 $\text{[math]}$ 与底面 $\text{[math]}$ 所成角的正弦值为 $\text{[math]}$ ．若球 $\text{[math]}$ 与三棱台 $\text{[math]}$ 内切（即球与棱台各面均相切）．
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的正切值；
3. （3）求四棱台 $\text{[math]}$ 的体积和球 $\text{[math]}$ 的表面积．
答案解析收藏纠错 + 选题
19. (2024高一下·湖州期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）写出函数 $\text{[math]}$ 的单调区间；
2. （2）若函数 $\text{[math]}$ 有两个不同零点，求实数 $\text{[math]}$ 的取值范围；
3. （3）已知点 $\text{[math]}$ ， $\text{[math]}$ 是函数 $\text{[math]}$ 图象上的两个动点，且满足 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题