一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
A . 6
B . 10
C . 12
D . 24
-
-
-
A . 1.5
B . 2
C . 2.5
D . 5
-
6.
(2023九上·紫金期中)
在不透明布袋中装有除颜色外其它完全相同的红、白玻璃球,其中白球有60个.同学们通过多次试验后发现摸到红色球的频率稳定在0.25左右,则袋中红球个数约为( )
A . 15个
B . 20个
C . 25个
D . 30个
-
-
8.
(2023九上·紫金期中)
为了学习宣传党的二十大精神,某校学生宣讲团赴社区宣讲.现从2名男生1名女生中任选2人,则恰好选中1名男生1名女生的概率为( )
-
9.
(2024八下·温州经济技术开发月考)
某校在操场东边开发出一块长、宽分别为

、

的矩形菜园(如图),作为劳动教育系列课程的实验基地之一.为了便于管理,现要在中间开辟一横两纵三条等宽的小道,剩下的用于种植,且种植面积为

. 设小道的宽为

, 根据题意可列方程为( )

-
10.
(2023九上·紫金期中)
如图,在正方形

中,

,

相交于点O,E,F分别为边

上的动点(点E,F不与线段

的端点重合)且

, 连接

. 在点E,F运动的过程中,有下列四个结论:①

始终是等腰直角三角形;②

面积的最小值是2;③至少存在一个

, 使得

的周长是

;④四边形

的面积始终是4.其中结论正确的有( )

A . ①②③
B . ②③④
C . ①②④
D . ①②③④
二、填空题:本大题共6小题,每小题3分,共18分.
-
-
12.
(2023九上·紫金期中)
如图,在△ABC中,D,E分别是AB,AC的中点,点F,G在边BC上,且DG=EF.只需添加一个条件即可证明四边形DFGE是矩形,这个条件可以是
.(写出一个即可)

-
13.
(2023九上·紫金期中)
做任意抛掷一只纸杯的重复试验,记录杯口朝上的次数,获得如下数据:
抛掷总次数 | 100 | 150 | 200 | 300 |
杯口朝上的频数 | 21 | 32 | 44 | 66 |
估计任意抛掷一只纸杯,杯口朝上的概率是 .
-
-
-
16.
(2023九上·紫金期中)
如图,已知正方形

、正方形

的边长分别为4,1,将正方形

绕点A旋转,连接

, 点M是

的中点,连接
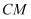
, 则线段
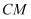
的最大值为
.

三、解答题:本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.
-
-
-
19.
(2023九上·紫金期中)
在一个不透明的袋子中装有4个小球,球上分别标有

, 0,1,2四个数字,这些小球除数字外都相同.
(1)从袋中任意摸出一个球,球上标有负数的概率是____________.
(2)小明先从袋子中任意摸出一个球(不放回),小华再从袋子里摸出另一个球,如果两球数字之差的绝对值小于或等于1,那么就称他俩“心有灵犀”,请用列表法(或画树状图)求两人“心有灵犀”的概率.
-
-
-
(1)
求证:四边形

是矩形;
-
(2)
若

, 求

的长.
-
22.
(2023九上·紫金期中)
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元.为了扩大销售,增加赢利,商场决定采取适当的降价措施.经调查发现,在一定范围内,每件衬衫的价格每降低1元,商场每天可多售出2件.如果商场通过销售这批衬衫每天要赢利1200元,每件衬衫的价格应降低多少元?
-
23.
(2024九上·龙华期末)
小颖和小红两位同学在做投掷骰子(质地均匀的正方体)试验,他们共做了60次试验,试验的结果如下表:
-
(1)
计算出现“3点朝上”的频率和“5点朝上”的频率.
-
(2)
小颖说:“根据试验得出,出现‘5点朝上’的机会最大.”小红说:“如果投掷600次,那么出现‘6点朝上’的次数正好是100次.”小颖和小红的说法正确吗?为什么?
-
24.
(2023九上·紫金期中)
在矩形

中,

,

, 点

从点

开始沿边

向终点

以

的速度移动;与此同时,点

从点

开始沿边

向终点

以

的速度移动,如果

,

分别从

,

同时出发,当点

运动到点

时,两点停止运动.设运动时间为

秒.

-
(1)
填空:

________

,

_________

(用含

的代数式表示);
-
-
(3)
是否存在

的值,使得五边形

的面积等于

?若存在,请求出此时

的值;若不存在,请说明理由.
-
-
(1)
如图2,当点M和点C重合时,过点C作

的垂线,垂足为点P,交直线

于点N.请直接写出

与

的数量关系:________.
-
(2)
如图3,过点M作

的垂线,垂足为点P,交直线

于点N,试证明(1)中的结论仍成立.
-
(3)
如图4,N为直线

上一点,若

, 请问是否始终能证明

?请说明理由.



