
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
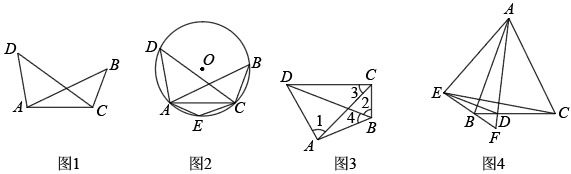
如图1所示,在线段同侧有两点
,
, 连接
,
,
,
, 如果
, 那么
,
,
,
四点在同一个圆上.

探究展示:
如图2所示,作经过点 ,
,
的
, 在劣弧
上取一点
(不与
,
重合),连接
,
,

则 , (依据
,
,
点
,
,
,
四点在同一个圆上,(对角互补的四边形四个顶点共圆)
点
,
在点
,
,
所确定的
上,(依据
点
,
,
,
四点在同一个圆上;
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:______;(从右边框内选一个选项,直接填序号)
依据2:______.(从右边框内选一个选项,直接填序号)
①圆内接四边形对角互补; ②对角互补的四边形四个顶点共圆; ③过不在同一直线上的三个点有且只有一个圆; ④经过两点的圆的圆心在这两点所连线段的垂直平分线上; |
(2)如图3所示,在四边形中,
,
, 则
的度数为______.

四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180° , 而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180° , 而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:


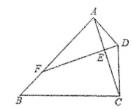

,
、
、
三点在以
为圆心,以
为半径的圆上.
填写数量关系

①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC;④BN
BM;⑤若AH
HD , 则S△BND
S△AHM . 其中正确的结论是( )


“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1,在线段AC同侧有两点B,D,连接 , 如果
, 那么A,B,C,D四点在同一个圆上.
探究展示:求证:点A,B,C,D四点在同一个圆上
如图2,作经过点A,C,D的 , 在劣弧
上取一点E(不与A,C重合),连接
,
, 则
.
①求证:A,D,B,E四点共圆;
②若 ,
的值是否会发生变化,若不变化,求出其值;若变化,请说明理由

(1)问题初现:如图1,在中,
, D是
外一点,且
, 则
;
思路:若以点A为圆心,为半径画
, 则点C、D必在
上,
是
的圆心角,而
是圆周角,从而可容易得到
的度数;
(2)问题解决:如图2,在四边形中,
, 求
的度数;
思路:可以通过证明A、B、C、D四点共圆,再利用圆周角的性质求出∠BAC的度数.请写出详细的解题过程.
(3)问题拓展:如图3,在中,
,
是
边上的高,且
, 则
.
如图 , 当
时,过点
作
交
于点
, 连接
, 则
的度数是,线段
与
的数量关系是.
如图2,若 , 点
是
上任一点
不与点
,
重合
, 过点
作
交
于点
, 过点
作
交
于点
, 连接
, 请写出
的度数及线段
与
的数量关系,并就图2的情形说明理由.
在(2)的条件下,将绕点
顺时针旋转得到
, 当点
,
,
在同一直线上,
时,请直接写出线段
的长.