江苏省泰州市兴化市顾庄学区三校联考2017年中考数学三模试卷

更新时间：2017-12-13 浏览次数：414 类型：中考模拟

一、选择题

1. (2018·弥勒模拟) 人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为（）

A . 77×10^﹣⁵ B . 0.77×10^﹣⁷ C . 7.7×10^﹣⁶ D . 7.7×10^﹣⁷

答案解析收藏纠错 + 选题
2. (2024九上·泸县月考) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2017·兴化模拟) 估计﹣1+ $\text{[math]}$ 的值（）

A . 在4和5之间 B . 在3和4之间 C . 在2和3之间 D . 在1和2之间

答案解析收藏纠错 + 选题
4. (2020九下·石嘴山月考) 如图是某几何体的三视图，该几何体是（）

A . 三棱柱 B . 长方体 C . 圆锥 D . 圆柱

答案解析收藏纠错 + 选题
5. 对于一组数据﹣1，﹣1，4，2，下列结论不正确的是（）

A . 平均数是1 B . 众数是﹣1 C . 中位数是0.5 D . 方差是3.5

答案解析收藏纠错 + 选题
6. (2017·兴化模拟) 已知关于x、y的方程组 $\text{[math]}$ ，给出下列说法：
①当a=1时，方程组的解也是方程x+y=2的一个解；
②当x﹣2y＞8时，a＞ $\text{[math]}$ ；
③不论a取什么实数，2x+y的值始终不变；
④若y=x²+5，则a=﹣4．以上说法正确的是（）

A . ②③④ B . ①②④ C . ③④ D . ②③

答案解析收藏纠错 + 选题

二、填空题

7. (2017·兴化模拟) ﹣27的立方根是．

答案解析收藏纠错 + 选题
8. (2023八上·开福开学考) 若正多边形的一个外角为40°，则这个正多边形是边形．

答案解析收藏纠错 + 选题
9. (2019·岳阳模拟) 分解因式：2x²﹣2y²=．

答案解析收藏纠错 + 选题
10. (2017·兴化模拟) 一只不透明袋子中装有2个红球、1个黄球，这些球除颜色外都相同．小明搅匀后从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出1个球．则两次摸出的球都是黄球的概率是．

答案解析收藏纠错 + 选题
11. (2017·兴化模拟) 一个三角板（含30°、60°角）和一把直尺摆放位置如图所示，直尺与三角板的一角相交于点A，一边与三角板的两条直角边分别相交于点D、点E，且CD=CE，点F在直尺的另一边上，那么∠BAF的大小为°．

答案解析收藏纠错 + 选题
12. (2017·兴化模拟) 在Rt△ABC中，AD是斜边BC边上的中线，G是△ABC重心，如果BC=6，那么线段AG的长为．

答案解析收藏纠错 + 选题
13. (2020·邯郸模拟) 已知a²+5ab+b²=0（a≠0，b≠0），则代数式 $\text{[math]}$ + $\text{[math]}$ 的值等于．

答案解析收藏纠错 + 选题
14. (2017·兴化模拟) 圆锥体的底面半径为2，侧面积为8π，则其侧面展开图的圆心角等于．

答案解析收藏纠错 + 选题
15. (2017·兴化模拟) 如图，抛物线y=x²﹣2x+k（k＜0）与x轴相交于A（x₁ ， 0）、B（x₂ ， 0）两点，其中x₁＜0＜x₂ ，当x=x₁+2时，y0（填“＞”“=”或“＜”号）．

答案解析收藏纠错 + 选题
16. (2017·兴化模拟) 在矩形ABCD中，AB=4，BC=3，点P在边AB上．若将△DAP沿DP折叠，使点A落在矩形ABCD的对角线上，则AP的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·兴化模拟) 计算题|1﹣ $\text{[math]}$ |﹣ $\text{[math]}$ +2cos30°﹣2017⁰；
1. （1）计算：|1﹣ $\text{[math]}$ |﹣ $\text{[math]}$ +2cos30°﹣2017⁰；
2. （2）解不等式组 $\text{[math]}$ 并求其最小整数解．
答案解析收藏纠错 + 选题
18. (2023·姜堰模拟) 某校为更好地开展“传统文化进校园”活动，随机抽查了部分学生，了解他们最喜爱的传统文化项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布条形图．
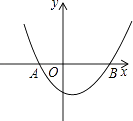
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题：
1. （1）直接写出频数分布表中a的值；
2. （2）补全频数分布条形图；
3. （3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？
答案解析收藏纠错 + 选题
19. (2019八下·泰兴期中) 某篮球运动员去年共参加40场比赛，其中3分球的命中率为0.25，平均每场有12次3分球未投中．
1. （1）该运动员去年的比赛中共投中多少个3分球？
2. （2）在其中的一场比赛中，该运动员3分球共出手20次，小亮说，该运动员这场比赛中一定投中了5个3分球，你认为小亮的说法正确吗？请说明理由．
答案解析收藏纠错 + 选题
20. (2017·兴化模拟) 如图，已知菱形ABCD的对角线AC，BD相交于点O，延长AB至点E，使BE=AB，连接CE．
1. （1）求证：四边形BECD是平行四边形；
2. （2）若∠E=60°，AC=4 $\text{[math]}$ ，求菱形ABCD的面积．
答案解析收藏纠错 + 选题
21. (2017·兴化模拟) 为了倡导节能低碳的生活，某公司对集体宿舍用电收费作如下规定：一间宿舍一个月用电量不超过a千瓦时，则一个月的电费为20元；若超过a千瓦时，则除了交20元外，超过部分每千瓦时要交 $\text{[math]}$ 元．某宿舍3月份用电80千瓦时，交电费35元；4月份用电45千瓦时，交电费20元．
1. （1）求a的值；
2. （2）若该宿舍5月份交电费45元，那么该宿舍当月用电量为多少千瓦时？
答案解析收藏纠错 + 选题
22. (2017·兴化模拟) 如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，∠AEO=∠C，OE交BC于点F．
1. （1）求证：OE∥BD；
2. （2）当⊙O的半径为5，sin∠DBA= $\text{[math]}$ 时，求EF的长．
答案解析收藏纠错 + 选题
23. (2017·兴化模拟) 如图，从A地到B地的公路需经过C地，图中AC=6千米，∠CAB=15°，∠CBA=30°．因城市规划的需要，将在A，B两地之间修建一条笔直的公路．
1. （1）求改直后的公路AB的长；
2. （2）问公路改直后该段路程比原来缩短了多少千米？（结果保留根号）
答案解析收藏纠错 + 选题
24. (2017·兴化模拟) 已知点A（1，2）、点 B在双曲线y= $\text{[math]}$ （x＞0）上，过B作BC⊥x轴于点C，如图，P是y轴上一点，
1. （1）求k的值及△PBC的面积；
2. （2）设点M（x₁ ， y₁）、N（x₂ ， y₂）（x₂＞x₁＞0）是双曲线y= $\text{[math]}$ （x＞0）上的任意两点，s= $\text{[math]}$ ，t= $\text{[math]}$ ，试判断s与t的大小关系，并说明理由．
答案解析收藏纠错 + 选题
25. (2017·兴化模拟) 如图，点A在直线l上，点Q沿着直线l以3厘米/秒的速度由点A向右运动，以AQ为边作Rt△ABQ，使∠BAQ=90°，tan∠ABQ= $\text{[math]}$ ，点C在点Q右侧，CQ=1厘米，过点C作直线m⊥l，过△ABQ的外接圆圆心O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF= $\text{[math]}$ CD，以DE、DF为邻边作矩形DEGF．设运动时间为t秒．
1. （1）直接用含t的代数式表示BQ、DF；
2. （2）当0＜t＜1时，求矩形DEGF的最大面积；
3. （3）点Q在整个运动过程中，当矩形DEGF为正方形时，求t的值．
答案解析收藏纠错 + 选题
26. (2017·兴化模拟) 已知抛物线y₁=a（x﹣x₁）（x﹣x₂）（a≠0，x₁≠x₂）与x轴分别交于A（x₁ ， 0）、
B（x₂ ， 0）两点，直线y₂=2x+t经过点A．
1. （1）已知A、B两点的横坐标分别为3、﹣1．
  ①当a=1时，直接写出抛物线y₁和直线y₂相应的函数表达式；
  ②如图，已知抛物线y₁在3＜x＜4这一段位于直线y₂的下方，在5＜x＜6这一段位于直线y₂的上方，求a的取值范围；
2. （2）若函数y=y₁+y₂的图象与x轴仅有一个公共点，探求x₂﹣x₁与a之间的数量关系．
答案解析收藏纠错 + 选题