2015-2016学年广东省揭阳市普宁市七年级下学期期末数学...

更新时间：2024-07-12 浏览次数：597 类型：期末考试

一、选择题

1. (2016七下·普宁期末) 下列各组角中，∠1与∠2是对顶角的为（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021七下·埇桥期末) 若□×2xy=16x³y² ，则□内应填的单项式是（　　）

A . 4x²y B . 8x³y² C . 4x²y² D . 8x²y

答案解析收藏纠错 + 选题
3. (2016七下·普宁期末) 计算（6×10³）•（8×10⁵）的结果是（）

A . 48×10⁹ B . 48×10¹⁵ C . 4.8×10⁸ D . 4.8×10⁹

答案解析收藏纠错 + 选题
4. (2016七下·普宁期末) 下列计算正确的是（）

A . （﹣x³）²=﹣x⁶ B . （﹣x²）³=﹣x⁶ C . x⁶÷x³=x² D . x³•x⁴=x¹²

答案解析收藏纠错 + 选题
5. (2023九上·盘锦开学考) 下面四个图形中，线段BE是△ABC的高的图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. 甲和乙一起做游戏，下列游戏规则对双方公平的是（）

A . 在一个装有2个红球和3个白球（每个球除颜色外都相同）的袋中任意摸出一球，摸到红球甲获胜，摸到白球乙获胜； B . 从标有号数1到100的100张卡片中，随意抽取一张，抽到号数为奇数甲获胜，否则乙获胜； C . 任意掷一枚质地均匀的骰子，掷出的点数小于4则甲获胜，掷出的点数大于4则乙获胜； D . 让小球在如图所示的地板上自由地滚动，并随机地停在某块方块上，若小球停在黑色区域则甲获胜，若停在白色区域则乙获胜

答案解析收藏纠错 + 选题
7. (2023七下·信宜期中) 下列各式不能运用平方差公式计算的是（）

A . （﹣x﹣y）（﹣x+y） B . （﹣x+y）（x﹣y） C . （x+y）（x﹣y） D . （y+x）（x﹣y）

答案解析收藏纠错 + 选题
8. (2016七下·普宁期末) 下列各式计算正确的是（）

A . （m﹣n）²=m²﹣n² B . （m+2）²=m²+2m+4 C . （ $\text{[math]}$ ﹣m）²= $\text{[math]}$ ﹣m+m² D . （﹣m+n）²=m²+2mn+n²

答案解析收藏纠错 + 选题
9. (2016七下·普宁期末) 如图，等腰△ABC中，AB=AC，沿直线MN折叠，使点A与点B重合，折痕MN与AC交于点D，已知∠DBC=15°，则∠A的度数是（）

A . 50° B . 45° C . 30° D . 15°

答案解析收藏纠错 + 选题

二、填空题

10. (2024八上·金平期中) 已知等腰三角形的两条边分别是3，6，则第三边的长为．

答案解析收藏纠错 + 选题
11. (2016七下·普宁期末) 计算：（﹣18a²b+10b²）÷（﹣2b）=．

答案解析收藏纠错 + 选题
12. (2016七下·普宁期末) 如图，转动的转盘停止转动后，指针指向黑色区域的概率是．

答案解析收藏纠错 + 选题
13. (2017八上·宁城期末) 如图，点B在AE上，∠CAB=∠DAB，要使△ABC≌△ABD，可补充的一个条件是：．（答案不唯一，写一个即可）

答案解析收藏纠错 + 选题
14. (2016七下·普宁期末) 已知圆锥的底面半径是2cm，那么圆锥的体积V（cm³）与高h（cm）的关系式是

答案解析收藏纠错 + 选题
15. (2016七下·普宁期末) 如图，Rt△ABC中，∠B=90°，CD是∠BCA的平分线，DE⊥AC于E，AC=10，BC=6，则AE=．

答案解析收藏纠错 + 选题

三、解答题（一）

16. (2016七下·普宁期末) 计算：[（3a+b）²﹣b²]÷a．

答案解析收藏纠错 + 选题
17. (2016七下·普宁期末) 化简求值：3x²+（﹣ $\text{[math]}$ x+ $\text{[math]}$ y²）（2x﹣ $\text{[math]}$ y），其中x=﹣ $\text{[math]}$ ，y= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021八上·南阳月考) 已知∠MAN．
1. （1）用尺规完成下列作图：（保留作图痕迹，不写作法）
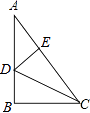
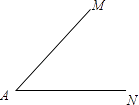
  ①作∠MAN的平分线AE；
  ②在AE上任取一点F，作AF的垂直平分线分别与AM、AN交于P、Q；
2. （2）在（1）的条件下，线段AP与AQ有什么数量关系，请直接写出结论．
答案解析收藏纠错 + 选题

四、解答题（二）

19. (2016七下·普宁期末) 手机微信推出了抢红包游戏，它有多种玩法，其中一种为“拼手气红包”，用户设定好总金额以及红包个数后，可以生成不等金额的红包．现有一用户发了三个“拼手气红包”，总金额为3元，随机被甲、乙、丙三人抢到．
1. （1）判断下列事件中，哪些是确定事件，哪些是不确定事件？
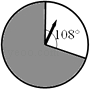
  ①丙抢到金额为1元的红包；
  ②乙抢到金额为4元的红包
  ③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多；
2. （2）记金额最多、居中、最少的红包分别为A，B，C．
  ①求出甲抢到红包A的概率；
  ②若甲没抢到红包A，则乙能抢到红包A的概率又是多少？
答案解析收藏纠错 + 选题
20. (2016七下·普宁期末) 把下列的推理过程补充完整，并在括号里填上推理的依据：
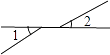
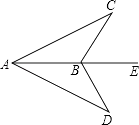
如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．
试说明：DF∥AB
解：因为BE是∠ABC的角平分线
所以（角平分线的定义）
又因为∠E=∠1（已知）
所以∠E=∠2（）
所以（）
所以∠A+∠ABC=180°（）
又因为∠3+∠ABC=180°（已知）
所以（同角的补角相等）
所以DF∥AB（）

答案解析收藏纠错 + 选题
21. (2016七下·普宁期末) 如图，在△ABC中，∠C=90°，点D是AB边上的一点，DE⊥AB于D，交AC于M，且ED=AC，过点E作EF∥BC分别交AB、AC于点F、N．
1. （1）试说明：△ABC≌△EFD；
2. （2）若∠A=25°，求∠EMN的度数．
答案解析收藏纠错 + 选题

五、解答题（三）

22. (2016七下·普宁期末) 陈杰骑自行车去上学，当他以往常的速度骑了一段路时，忽然想起要买某本书，于是又折回到刚经过的一家书店，买到书后继续赶去学校．以下是他本次上学离家距离与时间的关系示意图．根据图中提供的信息回答下列问题：
1. （1）陈杰家到学校的距离是米？陈杰在书店停留了分钟？本次上学途中，陈杰一共行驶了米？
2. （2）在整个上学的途中哪个时间段陈杰骑车速度最快？最快的速度是多少米？
3. （3）如果陈杰不买书，以往常的速度去学校，需要多少分钟？本次上学比往常多用多少分钟？
答案解析收藏纠错 + 选题
23. (2016七下·普宁期末) 观察下列各式：
（x﹣1）÷（x﹣1）=1；
（x²﹣1）÷（x﹣1）=x+1；
（x³﹣1）÷（x﹣1）=x²+x+1；
（x⁴﹣1）÷（x﹣1）=x³+x²+x+1；
（x⁸﹣1）÷（x﹣1）=x⁷+x⁶+x⁵+…+x+1；
1. （1）根据上面各式的规律填空：
  ①（x²⁰¹⁶﹣1）÷（x﹣1）=
  ②（xⁿ﹣1）÷（x﹣1）=
2. （2）利用②的结论求2²⁰¹⁶+2²⁰¹⁵+…+2+1的值；
3. （3）若1+x+x²+…+x²⁰¹⁵=0，求x²⁰¹⁶的值．
答案解析收藏纠错 + 选题
24. (2023八上·义乌月考) 如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．
1. （1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
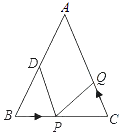
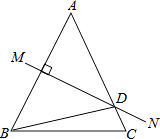
  ①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
  ②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
2. （2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2015-2016学年广东省揭阳市普宁市七年级下学期期末数学...

副标题：

*注意事项：

2015-2016学年广东省揭阳市普宁市七年级下学期期末数学...

试题分析

总体分析

题量分析

难度分析

知识点分析