尺码 | 39 | 40 | 41 | 42 | 43 |
平均每天销售数量/件 | 10 | 12 | 20 | 12 | 12 |
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是( )
引体向上数/个 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数 | 1 | 1 | 2 | 1 | 3 | 3 | 2 | 1 | 1 |
这15名男同学引体向上数的中位数是( )
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
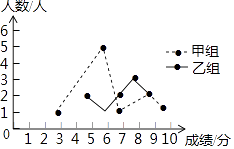
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
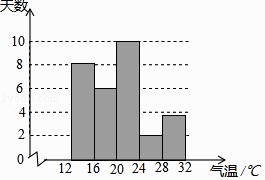
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
