2016-2017学年辽宁省营口市大石桥市水源中学九年级上学...

更新时间：2016-12-19 浏览次数：1355 类型：期中考试

一、选择题

1. 有下列关于x的方程：①ax²+bx+c=0，②3x（x﹣4）=0，③x²+y﹣3=0，④ $\text{[math]}$ +x=2，⑤x³﹣3x+8=0，⑥ $\text{[math]}$ x²﹣5x+7=0，⑦（x﹣2）（x+5）=x²﹣1．其中是一元二次方程的有（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
2. (2021九上·龙泉期中) 下面所列图形中是中心对称图形的为（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021九上·薛城期中) 已知关于x的一元二次方程x²+mx+n=0的两个实数根分别为x₁=﹣2，x₂=4，则m+n的值是（）

A . ﹣10 B . 10 C . ﹣6 D . 2

答案解析收藏纠错 + 选题
4. (2016九上·大石桥期中) 如图，AB为圆O的直径，BC为圆O的一弦，自O点作BC的垂线，且交BC于D点．若AB=16，BC=12，则△OBD的面积为何？（）

A . 6 $\text{[math]}$ B . 12 $\text{[math]}$ C . 15 D . 30

答案解析收藏纠错 + 选题
5. (2016九上·大石桥期中) 若关于x的一元二次方程为ax²+bx+6=0（a≠0）的解是x=1，则2016﹣a﹣b的值是（）

A . 2020 B . 2008 C . 2014 D . 2022

答案解析收藏纠错 + 选题
6. (2017·新泰模拟) 某同学在用描点法画二次函数y=ax²+bx+c的图象时，列出下面的表格：
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
﹣7.5
﹣2.5
0.5
1.5
0.5
…
根据表格提供的信息，下列说法错误的是（）

A . 该抛物线的对称轴是直线x=﹣2 B . 该抛物线与y轴的交点坐标为（0，﹣2.5） C . b²﹣4ac=0 D . 若点A（0.5，y₁）是该抛物线上一点．则y₁＜﹣2.5

答案解析收藏纠错 + 选题
7. (2017·天山模拟) 已知2是关于x的方程x²﹣2mx+3m=0的一个根，并且这个方程的两个根恰好是等腰三角形ABC的两条边长，则三角形ABC的周长为（）

A . 10 B . 14 C . 10或14 D . 8或10

答案解析收藏纠错 + 选题
8. (2016九上·大石桥期中) 已知点A（a，2015）与点A′（﹣2016，b）是关于原点O的对称点，则a+b的值为（）

A . 1 B . 5 C . 6 D . 4

答案解析收藏纠错 + 选题
9. (2016九上·大石桥期中) 如图，AB是⊙O的直径，点D是弧 $\text{[math]}$ 的中点，∠ABC=52°，则∠DAB等于（）

A . 58° B . 61° C . 72° D . 64°

答案解析收藏纠错 + 选题
10. (2016九上·大石桥期中) 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，下列给出四个结论中，正确结论的个数是（）个
①c＞0；
②若点B（﹣ $\text{[math]}$ ，y₁）、C（﹣ $\text{[math]}$ ，y₂）为函数图象上的两点，则y₁＜y₂；
③2a﹣b=0；
④ $\text{[math]}$ ＜0；
⑤4a﹣2b+c＞0．

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题

二、填空题

11. (2019九上·施秉月考) 一元二次方程（a+1）x²﹣ax+a²﹣1=0的一个根为0，则a=．

答案解析收藏纠错 + 选题
12. (2023九上·静海月考) 已知函数 $\text{[math]}$ 是关于x的二次函数，则m的值为．

答案解析收藏纠错 + 选题
13. (2016九上·大石桥期中) 如图，已知点A（0，1），B（0，﹣1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于度．

答案解析收藏纠错 + 选题
14. (2016九上·大石桥期中) 在平面直角坐标系中，将函数y=﹣2x²的图象先向右平移1个单位长度，再向上平移5个单位长度，所得图象的函数表达式是．

答案解析收藏纠错 + 选题
15. (2016九上·大石桥期中) 若实数a、b满足（4a+4b）（4a+4b﹣2）﹣8=0，则a+b=．

答案解析收藏纠错 + 选题
16. (2016九上·大石桥期中) 一个y关于x的函数同时满足两个条件：①图象过（2，1）点；②当x＞0时，y随x的增大而减小．这个函数解析式为．（写出一个即可）

答案解析收藏纠错 + 选题
17. (2016九上·大石桥期中) 如图，DE是△ABC的中位线，M是DE的中点，那么 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
18. (2016九上·大石桥期中) 如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（ $\text{[math]}$ ，0），B（0，2），则点B₂₀₁₇的坐标为．

答案解析收藏纠错 + 选题

三、解答题

19. (2016九上·大石桥期中) 先化简，再求值：（ $\text{[math]}$ + $\text{[math]}$ ）÷ $\text{[math]}$ ，其中a满足a²﹣4a﹣6=0．

答案解析收藏纠错 + 选题
20. (2016九上·封开期中) 每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，
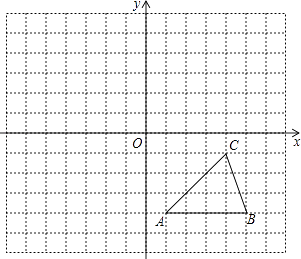
①写出A、B、C的坐标．
②以原点O为对称中心，画出△ABC关于原点O对称的△A₁B₁C₁ ，并写出A₁、B₁、C₁ ．

答案解析收藏纠错 + 选题
21. (2016九上·大石桥期中) 如图所示，⊙O的内接△ABC中，∠BAC=45°，∠ABC=15°，AD∥OC并交BC的延长线于D点，OC交AB于E点．
1. （1）求∠D的度数；
2. （2）求证：AC²=AD•CE．
答案解析收藏纠错 + 选题
22. (2016九上·大石桥期中) 某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长37米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的面积最大？如图是两位学生争议的情境：请根据上面的信息，解决问题：
1. （1）设AB=x米（x＞0），试用含x的代数式表示BC的长；
2. （2）请你判断谁的说法正确，为什么？
答案解析收藏纠错 + 选题
23. (2016九上·大石桥期中) 小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD=1.2m，CE=0.8m，CA=30m（点A，E，C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB．（结果精确到0.1m）

答案解析收藏纠错 + 选题
24. (2016九上·大石桥期中) 某商店原来平均每天可销售某种水果100千克，每千克可盈利7元，为减少库存，经市场调查，如果这种水果每千克降价1元，则每天可所多售出20千克．
1. （1）设每千克水果降价x元，平均每天盈利y元，试写出y关于x的函数表达式；
2. （2）若要平均每天盈利400元，则每千克应降价多少元？
3. （3）每千克降价多少元时，每天的盈利最多？最多盈利多少元？
答案解析收藏纠错 + 选题
25. (2016九上·大石桥期中) 如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，联结AD，以AD为一边且在AD的右侧作正方形ADEF．
1. （1）如果AB=AC，∠BAC=90°，
  ①当点D在线段BC上时（与点B不重合），如图2，将△ABD绕A点逆时针旋转90°，所得到的三角形为，线段CF，BD所在直线的位置关系为，线段CF，BD的数量关系为；
2. （2） ②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
3. （3）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C，F不重合），并说明理由．
答案解析收藏纠错 + 选题
26. (2016九上·大石桥期中) 如图，已知二次函数y=﹣x²+bx+c（b，c为常数）的图象经过点A（5，3），点C（0，8），顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BC．
1. （1）求该二次函数的解析式及点M的坐标；
2. （2）求△ABC的面积；
3. （3）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围．
答案解析收藏纠错 + 选题