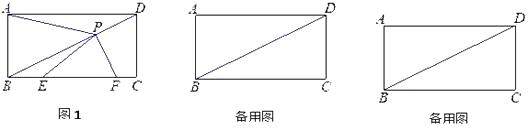
 B .
B .  C .
C .  D .
D . 

计算:(﹣ )÷(
﹣
+
﹣
)
方法一:原式=(﹣ )÷[(
+
)﹣(
+
)]=(﹣
)÷(
﹣
)=﹣
×3=﹣
方法二:原式的倒数为( ﹣
+
﹣
)÷(﹣
)=(
﹣
+
﹣
)×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=﹣
通过阅读以上解题过程,你认为哪种方法更简单,选择合适的方法计算下题:
(﹣ )÷(
﹣
+
﹣
).
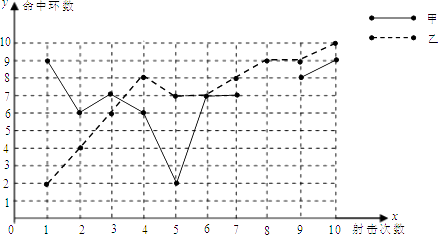
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图