2018年浙江省湖州市中考数学冲刺模拟卷（3）

如图，等边三角形ABC内接于⊙O，若边长为4cm，则⊙O的半径为（　　）

①如果一组数据的众数是5，那么这组数据中出现次数最多的数是5；

②如果一组数据的平均数是0，那么这组数据的中位数为0；

③如果一组数据1，2，x，4的中位数是3，那么x=4；

④如果一组数据的平均数是正数，那么这组数据都是正数．

其中错误的个数是（  ）

如图，在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD于O，AE⊥BC，DF⊥BC，垂足分别为E、F，AD=4，BC=8，则AE+EF等于(　　)

如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3：3：2：2的比确定，应该录取（填“甲”或“乙”）

如图，在矩形ABCD中，AB=4，AD=2，以点A为圆心，AB长为半径画圆弧交边DC于点E，则的长度为 .

已知抛物线y=ax²﹣4ax+c经过点A（0，2），顶点B的纵坐标为3．将直线AB向下平移，与x轴、y轴分别交于点C、D，与抛物线的一个交点为P，若D是线段CP的中点，则点P的坐标为 ．

如图，有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ，连接EF、GH得到四边形EFGH，设S_{四边形ABCD}=S₁ ， S_{四边形EFGH}=S₂ ， S_{四边形MNPQ}=S₃ ， 若S₁+S₂+S₃=10，则S₂=  ．

如图，AB是⊙O的直径，C是的中点，CE⊥AB于E，BD交CE于点F，

（1）求证：CF＝BF；
（2）若CD＝12，AC＝16，求⊙O的半径和CE的长。

对雾霾了解程度的统计表：

请结合统计图表，回答下列问题．

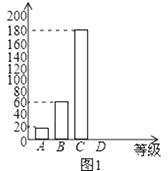
对雾霾天气了解程度的条形统计图

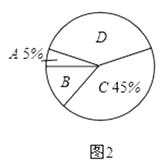
对雾霾天气了解程度的扇形统计图

如图①，△ABC的角平分线BD、CE相交于点P.
（1）如果∠A=70°，求∠BPC的度数；
（2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；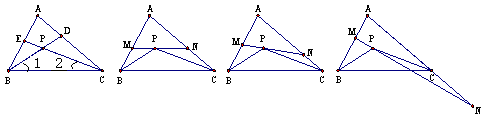

①                   ②             ③            ④
在（2）的条件下，将直线MN绕点P旋转.
（ⅰ）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；
（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由.

如图，已知抛物线y=ax²+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．