2018年浙江省嘉兴市中考数学冲刺模拟卷（1）

更新时间：2018-05-23 浏览次数：398 类型：中考模拟

一、选择题

1. (2023七上·嵊州期中) 计算（﹣9）﹣（﹣3）的结果是（）

A . ﹣12 B . ﹣6 C . +6 D . 12

答案解析收藏纠错 + 选题
2. 在下列四个图案中，不是中心对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 2016年12月11日，我国风云四号卫星发射成功，它将停留在距离地面36000公里高的太空，专门用于对固定区域进行气象遥感探测．数据36000用科学记数法表示（）

A . 3.6×10³公里 B . 3.6×10⁴公里 C . 36×10³公里 D . 36×10⁴公里

答案解析收藏纠错 + 选题
4. (2016九上·莒县期中) 某科研小组为了考查某河流野生鱼的数量，从中捕捞200条，作上标记后，放回河里，经过一段时间，再从中捕捞300条，发现有标记的鱼有15条，则估计该河流中有野生鱼（）

A . 8000条 B . 4000条 C . 2000条 D . 1000条

答案解析收藏纠错 + 选题
5. (2017九上·青龙期末) 如图，若DC∥FE∥AB，则有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 设 $\text{[math]}$ 的小数部分为b，那么（4+b）b的值是（　　）

A . 1 B . 是一个有理数 C . 3 D . 无法确定

答案解析收藏纠错 + 选题
7. (2017·江汉模拟) 如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ的最小值（）

A . 5 B . 4 $\text{[math]}$ C . 4.75 D . 4.8

答案解析收藏纠错 + 选题
8. (2017·个旧模拟) 不等式x﹣3≤3x+1的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2018·广水模拟)
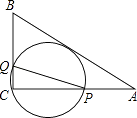
下面是小明按照语句画出的四个图形：（1）直线EF经过点C；（2）点A在直线l外；（3）经过点O的三条线段a、b、c；（4）线段AB、CD相交于点B．他所画图形中，正确的个数是（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2017九上·邗江期末)
如图，分别过点P_i（i，0）（i=1、2、…、n）作x轴的垂线，交 $\text{[math]}$ 的图象于点A_i ，交直线 $\text{[math]}$ 于点B_i ．则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021·靖江模拟) 分解因式：xy²﹣2xy+x=．

答案解析收藏纠错 + 选题
12. 已知A，B两地相距160km，一辆汽车从A地到B地的速度比原来提高了25%，结果比原来提前0.4h到达，这辆汽车原来的速度是 km/h．

答案解析收藏纠错 + 选题
13. 现有四张分别标有数字1，2，3，4的卡片，它们除数字外完全相同，把卡片背面朝上洗匀，从中随机抽取一张后放回，再背面朝上洗匀，从中随机抽取一张，则两次抽出的卡片所标数字不同的概率是

答案解析收藏纠错 + 选题
14. (2022八下·牡丹江期中) 如图，在矩形ABCD中，AB=8，BC=16，将矩形ABCD沿EF折叠，使点C与点A重合，则折痕EF的长为．

答案解析收藏纠错 + 选题
15. (2017七上·温江期末) 一个幻方中，每一行，每一列，及每一对角线上的三个数之和有相同的值，如图所示已知一个幻方中的三个数，x的值是．

答案解析收藏纠错 + 选题
16. (2017·鹤壁模拟) 如图，直径为10的⊙A经过点C（0，5）和点0（0，0），B是y轴右侧⊙A优弧上一点，则∠OBC的余弦值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017七下·嘉兴期中) 计算。
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2017·浙江模拟) 观察下表：
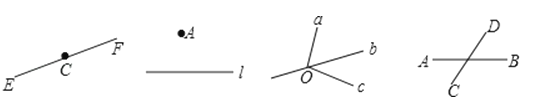
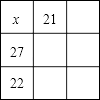
序号
1
2
3
…
图形
x　x
y
x　x
x　x　x
y　y
x　x　x
y　y
x　x　x
x　x　x　x
y　y　y
x　x　x　x
y　y　y
x　x　x　x
y　y　y
x　x　x　x
…
我们把某格中字母和所得到的多项式称为特征多项式，例如第1格的“特征多项式”为4x＋y.回答下列问题：
1. （1）第3格的“特征多项式”为，第4格的“特征多项式”为，第n格的“特征多项式”为；
2. （2）若第1格的“特征多项式”的值为－10，第2格的“特征多项式”的值为－16.
  ①求x，y的值；
  ②在此条件下，第n个特征多项式是否有最小值？若有，求出最小值和相应的n值．若没有，请说明理由．
答案解析收藏纠错 + 选题
19. (2017·南岗模拟) 已知四边形ABCD是正方形，点E、F分别在边AB、边BC上，DE⊥AF，DE与AF交于点O，将线段AE沿AF进行平移至FG，过点G作GH⊥AB的延长线于点H．
1. （1）判断四边形BFGH的形状并证明；
2. （2）写出图中所有面积相等的图形．
答案解析收藏纠错 + 选题
20.
如图，一次函数y=x+2的图象与反比例函数y= $\text{[math]}$ （k≠0）的图象交于A，B两点，且点A的坐标为（1，m）．
（1）求反比例函数y= $\text{[math]}$ （k≠0）的表达式；
（2）若P是y轴上一点，且满足△ABP的面积为6，求点P的坐标．

答案解析收藏纠错 + 选题
21. (2024八下·柯桥期中) 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
1. （1）写出表格中a，b，c的值；
2. （2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
答案解析收藏纠错 + 选题
22. (2021·昆山模拟) 如图，一艘渔船位于码头M的南偏东45°方向，距离码头120海里的B处，渔船从B处沿正北方向航行一段距离后，到达位于码头北偏东60°方向的A处．
1. （1）求渔船从B到A的航行过程中与码头M之间的最小距离．
2. （2）若渔船以20海里/小时的速度从A沿AM方向行驶，求渔船从A到达码头M的航行时间．
答案解析收藏纠错 + 选题
23. (2018九上·吴兴期末) 某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部△CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．
1. （1）当MN和AB之间的距离为0.5米时，求此时△EMN的面积；
2. （2）设MN与AB之间的距离为x 米，试将△EMN的面积S（平方米）表示成关于x的函数；
3. （3）请你探究△EMN的面积S（平方米）有无最大值，若有，请求出这个最大值；若没有，请说明理由．
答案解析收藏纠错 + 选题
24. (2021九上·昆都仑月考) 如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．
1. （1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
2. （2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．
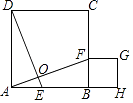
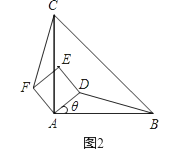
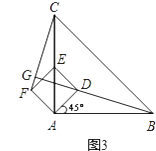
  ①求证：BD⊥CF；
  ②当AB=4，AD= $\text{[math]}$ 时，求线段BG的长．
答案解析收藏纠错 + 选题