2018年浙江省金华市中考数学冲刺模拟卷（1）

更新时间：2018-05-24 浏览次数：532 类型：中考模拟

一、选择题

1. (2016七上·重庆期中) 已知a，b互为相反数，c，d互为倒数，|e|= $\text{[math]}$ ，则代数式5（a+b）²+ $\text{[math]}$ cd﹣2e的值为（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·龙华模拟) 一个几何体由若干大小相同的小立方块搭成，图分别是从它的正面、上面看到的形状图，则搭成该几何体的小立方块至少需要（）

A . 5 块 B . 6 块 C . 7 块 D . 8 块

答案解析收藏纠错 + 选题
3. 以下列各组长度的线段为边，能构成三角形的是（）

A . 3cm、4cm、8cm B . 5cm、5cm、11cm C . 12cm、5cm、6cm D . 8cm、6cm、4cm

答案解析收藏纠错 + 选题
4.
如图，△ABC的三个顶点在正方形网格的格点上，则tan∠A的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2016·历城模拟) 下列计算正确的是（）

A . a²•a³=a⁶ B . a⁶÷a³=a² C . 4x²﹣3x²=1 D . （﹣2a²）³=﹣8a⁶

答案解析收藏纠错 + 选题
6. (2017九上·莒南期末) 由二次函数y=2（x﹣3）²+1，可知（）

A . 其图象的开口向下 B . 其图象的对称轴为直线x=﹣3 C . 其最小值为1 D . 当x＜3时，y随x的增大而增大

答案解析收藏纠错 + 选题
7. 若小李同学掷出的铅球在场地航砸出一个直径为10厘米，深2厘米的小坑，则该铅球的直径为（　　）

A . 20厘米 B . 19.5厘米 C . 14.5厘米 D . 10厘米

答案解析收藏纠错 + 选题
8. (2017七下·山西期末)
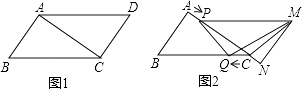
如图，有甲、乙两种地板样式，如果小球分别在上面自由滚动，设小球在甲种地板上最终停留在黑色区域的概率为P₁ ，在乙种地板上最终停留在黑色区域的概率为P₂ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 以上都有可能

答案解析收藏纠错 + 选题
9. (2017七下·滦南期末) 若关于 $\text{[math]}$ 的一元一次不等式组 $\text{[math]}$ 无解，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ ≥1 B . $\text{[math]}$ ＞1 C . $\text{[math]}$ ≤ $\text{[math]}$ D . $\text{[math]}$ ＜ $\text{[math]}$

答案解析收藏纠错 + 选题
10.
如左图，图1表示正六棱柱形状的高式建筑物，图2中的正六边形部分是从该建筑物的正上方看到的俯视图，P、Q、M、N表示小明在地面上的活动区域．小明想同时看到该建筑物的三个侧面，他应在（）

A . P区域 B . Q区域 C . M区域 D . N区域

答案解析收藏纠错 + 选题

二、填空题

11. 分解因式：x²﹣（x﹣3）²=．

答案解析收藏纠错 + 选题
12. (2018七上·酒泉期末) 已知 $\text{[math]}$ 则 $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2017九下·丹阳期中) 某广告公司全体员工年薪的具体情况如表：
年薪/万元
25
15
10
6
4
人数
1
1
3
3
2
则该公司全体员工年薪的中位数是万元

答案解析收藏纠错 + 选题
14. (2017七下·大冶期末) 如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为．

答案解析收藏纠错 + 选题
15. (2017·长春) 如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标为（2，1），（6，1），∠BAC=90°，AB=AC，直线AB交x轴于点P．若△ABC与△A'B'C'关于点P成中心对称，则点A'的坐标为．

答案解析收藏纠错 + 选题
16. 如图，在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上，C点在斜边上，设矩形的一边AB=xm，矩形的面积为ym² ，则y的最大值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·兰山模拟) 计算：（ $\text{[math]}$ ）^﹣2﹣（ $\text{[math]}$ ﹣ $\text{[math]}$ ）⁰+2sin30°+|﹣3|．

答案解析收藏纠错 + 选题
18. (2016八上·道真期末) 解方程 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2017九上·鸡西期末) 如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：

①将△ABC向上平移3个单位长度，画出平移后的△A₁B₁C₁ ，写出A₁、C₁的坐标；②将△A₁B₁C₁绕B₁逆时针旋转90°，画出旋转后的△A₂B₁C₂ ，求线段B₁C₁旋转过程中扫过的面积（结果保留π）．

答案解析收藏纠错 + 选题
20. (2018·东莞模拟) 企业举行“爱心一日捐”活动，捐款金额分为五个档次，分别是50元，100元，150元，200元，300元．宣传小组随机抽取部分捐款职工并统计了他们的捐款金额，绘制成两个不完整的统计图，请结合图表中的信息解答下列问题：
1. （1）宣传小组抽取的捐款人数为人，请补全条形统计图；
2. （2）在扇形统计图中，求100元所对应扇形的圆心角的度数；
3. （3）已知该企业共有500人参与本次捐款，请你估计捐款总额大约为多少元？
答案解析收藏纠错 + 选题
21. (2017九上·湖州月考) 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）²+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．
1. （1）当a=﹣ $\text{[math]}$ 时，
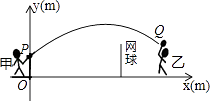
  ①求h的值；
  ②通过计算判断此球能否过网．
2. （2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为 $\text{[math]}$ m的Q处时，乙扣球成功，求a的值．
答案解析收藏纠错 + 选题
22. (2017·广州模拟) 如图，在 Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．
1. （1）求证：AE=BF．
2. （2）连接GB，EF，求证：GB∥EF．
3. （3）若AE=1，EB=3，求DG的长．
答案解析收藏纠错 + 选题
23. (2018九下·鄞州月考) 如图1，点P为四边形ABCD所在平面上的点，如果∠PAD=∠PBC，则称点P为四边形ABCD关于A、B的等角点，以点C为坐标原点，BC所在直线为x轴建立平面直角坐标系，点B的横坐标为﹣6．
1. （1）如图2，若A、D两点的坐标分别为A（﹣6，4）、D（0，4），点P在DC边上，且点P为四边形ABCD关于A、B的等角点，则点P的坐标为；
2. （2）如图3，若A、D两点的坐标分别为A（﹣2，4）、D（0，4）．
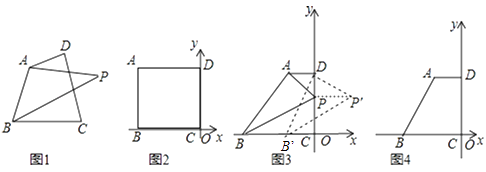
  ①若P在DC边上时，求四边形ABCD关于A、B的等角点P的坐标；
  ②在①的条件下，将PB沿x轴向右平移m个单位长度（0＜m＜6）得到线段P′B′，连接P′D，B′D，试用含m的式子表示P′D²+B′D² ，并求出使P′D²+B′D²取得最小值时点P′的坐标；
  ③如图4，若点P为四边形ABCD关于A、B的等角点，且点P坐标为（1，t），求t的值；
  ④以四边形ABCD的一边为边画四边形，所画的四边形与四边形ABCD有公共部分，若在所画的四边形内存在一点P，使点P分别是各相邻两顶点的等角点，且四对等角都相等，请直接写出所有满足条件的点P的坐标．
答案解析收藏纠错 + 选题
24. (2017·石家庄模拟)
如图1所示，在▱ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿射线AC的方向匀速平移得到△PNM，速度为1cm/s，同时，点Q从点C出发，沿射线CB方向匀速运动，速度为1cm/s，当△PNM停止平移时，点Q也停止运动，如图2所示，设运动时间为t（s）（0＜t＜4）．
1. （1）当t为何值时，PQ∥MN？
2. （2）设△QMC的面积为y（cm²），求y与t之间的函数关系式；
3. （3）是否存在某一时刻t，使得PQ=QM，若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题