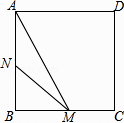
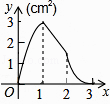
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
 B .
B .  C .
C . 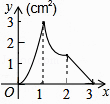 D .
D . 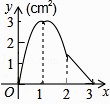

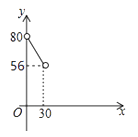 B .
B . 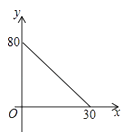 C .
C . 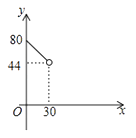 D .
D . 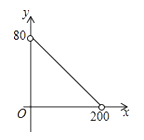
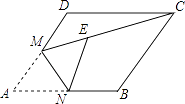
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
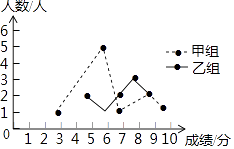
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
(说明:补全表格时相关数值保留一位小数)

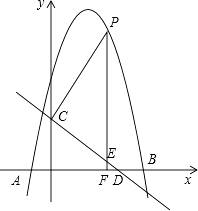
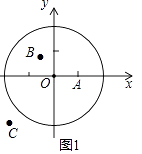
A(1,0)的距离跨度;
B(﹣ ,
)的距离跨度;
C(﹣3,﹣2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是.