北京市2018年中考数学试卷

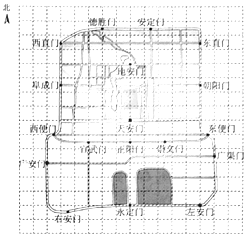
①当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（ ， ）时，表示左安门的点的坐标为（5， ）；②当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（ ， ）时，表示左安门的点的坐标为（10， ）；③当表示天安门的点的坐标为（1，1），表示广安门的点的坐标为（ ， ）时，表示左安门的点的坐标为（ ， ）；④当表示天安门的点的坐标为（ ， ），表示广安门的点的坐标为（ ， ）时，表示左安门的点的坐标为（ ， ）．上述结论中，所有正确结论的序号是（    ）

早高峰期间，乘坐（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．

已知：直线及直线外一点 ．

求作： ，使得 ．

作法：如图，

①在直线上取一点 ，作射线 ，以点 为圆心， 长为半径画弧，交 的延长线于点 ；

②在直线上取一点 （不与点 重合），作射线 ，以点 为圆心， 长为半径画弧，交 的延长线于点 ；

③作直线 ．

所以直线 就是所求作的直线．

根据小东设计的尺规作图过程，

小腾根据学习函数的经验，分别对函数 ， 随自变量 的变化而变化的规律进行了探究．

下面是小腾的探究过程，请补充完整：

．A课程成绩的频数分布直方图如下（数据分成6组： ， ， ， ， ， ）；

．A课程成绩在 这一组是：

70  71  71  71  76  76  77  78       79  79  79 

．A，B两门课程成绩的平均数、中位数、众数如下：

根据以上信息，回答下列问题：

已知点 （ ，6）， （ ， ）， （6， ）．