 B .
B .  C .
C .  D .
D . 
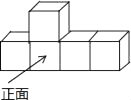
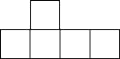 C .
C . 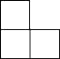
成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中的信息判断,下列结论中错误的是( )
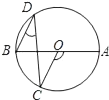
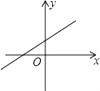 B .
B . 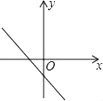 C .
C . 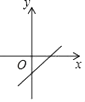 D .
D . 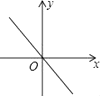
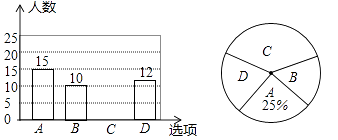
回答下列问题:
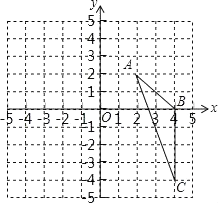
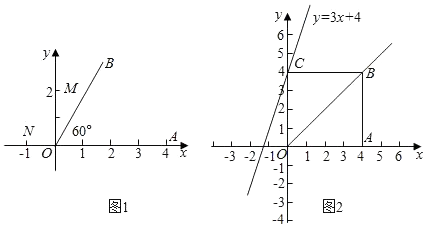
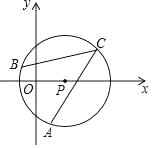
①请在图中,画出△ABC绕着点O逆时针旋转90°后得到的△A1B1C1,则∠A1C1B1的正切值=.
②以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴左侧,画出△A2B2C2 , 若点P(m,n)是△ABC上的任意一点,则变换后的对应点P′的坐标是.