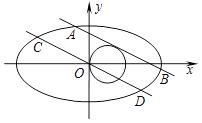2017年安徽省淮北市高考数学一模试卷（理科）

更新时间：2017-02-24 浏览次数：993 类型：高考模拟

一、选择题

1. (2017·淮北模拟) 已知集合P=（﹣∞，0]∪（3，+∞），Q={0，1，2，3}，则（∁_RP）∩Q=（）

A . {0，1} B . {0，1，2} C . {1，2，3} D . {x|0≤x＜3}

答案解析收藏纠错 + 选题
2. (2017·淮北模拟) 复数 $\text{[math]}$ 的共轭复数的模为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
3. (2017·泰安模拟) 已知x，y满足线性约束条件 $\text{[math]}$ ，若z=x+4y的最大值与最小值之差为5，则实数λ的值为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
4. (2017·淮北模拟) 函数f（x）=|x|+ $\text{[math]}$ （其中a∈R）的图像不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017·淮北模拟) 已知三个数1，a，9成等比数列，则圆锥曲线 $\text{[math]}$ 的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019高三上·大庆期中) 在△ABC中， $\text{[math]}$ ，则△ABC的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2017·淮北模拟) 下列说法正确的是（）
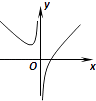
（1．）已知等比数列{a_n}，则“数列{a_n}单调递增”是“数列{a_n}的公比q＞1”的充分不必要条件；
（2．）二项式 $\text{[math]}$ 的展开式按一定次序排列，则无理项互不相邻的概率是 $\text{[math]}$ ；
（3．）已知 $\text{[math]}$ ，则 $\text{[math]}$ ；
（4．）为了解1000名学生的学习情况，采用系统抽样的方法，从中抽取容量为40的样本，则分段的间隔为40．

A . （1）（2） B . （2）（3） C . （1）（3） D . （2）（4）

答案解析收藏纠错 + 选题
8. (2017·淮北模拟) 执行如图的程序框图，则输出S的值为（）

A . $\text{[math]}$ ﹣67 B . $\text{[math]}$ ﹣67 C . $\text{[math]}$ ﹣68 D . $\text{[math]}$ ﹣68

答案解析收藏纠错 + 选题
9. (2016高一下·大名开学考) 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2017·淮北模拟) 若函数f（x）在其图像上存在不同的两点A（x₁ ， y₁），B（x₂ ， y₂），其坐标满足条件：|x₁x₂+y₁y₂|﹣ $\text{[math]}$ 的最大值为0，则称f（x）为“柯西函数”，
则下列函数：
①f（x）=x+ $\text{[math]}$ （x＞0）；
②f（x）=lnx（0＜x＜3）；
③f（x）=2sinx；
④f（x）= $\text{[math]}$ ．
其中为“柯西函数”的个数为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
11. (2017·淮北模拟) 已知直线l₁与圆心为C的圆（x﹣1）²+（y﹣2）²=4相交于不同的A，B两点，对平面内任意点Q都有 $\text{[math]}$ ，λ∈R，又点P为直线l₂：3x+4y+4=0上的动点，则 $\text{[math]}$ 的最小值为（）

A . 21 B . 9 C . 5 D . 0

答案解析收藏纠错 + 选题
12. (2017·淮北模拟) 已知定义在（0，+∞）的函数f（x），其导函数为f′（x），满足：f（x）＞0且 $\text{[math]}$ 总成立，则下列不等式成立的是（）

A . e^2e⁺³f（e）＜e^2ππ³f（π） B . e^2e⁺³f（π）＞e^2ππ³f（e） C . e^2e⁺³f（π）＜e^2ππ³f（e） D . e^2e⁺³f（e）＞e^2ππ³f（π）

答案解析收藏纠错 + 选题

二、填空题

13. (2017·淮北模拟) 已知实数a，b均大于0，且 $\text{[math]}$ 总成立，则实数m的取值范围是．

答案解析收藏纠错 + 选题
14. (2017·日照模拟) 设随机变量ξ服从正态分布N（2，9），若P（ξ＞c+1）=P（ξ＜c﹣1），则c=．

答案解析收藏纠错 + 选题
15. (2017·淮北模拟) 函数 $\text{[math]}$ 的值域是．

答案解析收藏纠错 + 选题
16. (2017·淮北模拟) 等差数列{a_n}的前n项和为S_n ，数列{b_n}是等比数列，且满足a₁=3，b₁=1，b₂+S₂=10，a₅﹣2b₂=a₃ ，数列{ $\text{[math]}$ }的前n项和T_n ，若T_n＜M对一切正整数n都成立，则M的最小值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·淮北模拟) 在△ABC中，设边a，b，c所对的角为A，B，C，且A，B，C都不是直角，（bc﹣8）cosA+accosB=a²﹣b² ．
（Ⅰ）若b+c=5，求b，c的值；
（Ⅱ）若 $\text{[math]}$ ，求△ABC面积的最大值．

答案解析收藏纠错 + 选题
18. (2017·淮北模拟) 为调查了解某省属师范大学师范类毕业生参加工作后，从事的工作与教育是否有关的情况，该校随机调查了该校80位性别不同的2016年师范类毕业大学生，得到具体数据如表：
与教育有关
与教育无关
合计
男
30
10
40
女
35
5
40
合计
65
15
80
1. （1）能否在犯错误的概率不超过5%的前提下，认为“师范类毕业生从事与教育有关的工作与性别有关”？
  参考公式： $\text{[math]}$ （n=a+b+c+d）．
  附表：
  P（K²≥k₀）
  0.50
  0.40
  0.25
  0.15
  0.10
  0.05
  0.025
  0.010
  k₀
  0.455
  0.708
  1.323
  2.072
  2.706
  3.841
  5.023
  6.635
2. （2）求这80位师范类毕业生从事与教育有关工作的频率；
3. （3）以（2）中的频率作为概率．该校近几年毕业的2000名师范类大学生中随机选取4名，记这4名毕业生从事与教育有关的人数为X，求X的数学期望E（X）．
答案解析收藏纠错 + 选题
19. (2017·淮北模拟) 正三棱柱ABC﹣A₁B₁C₁底边长为2，E，F分别为BB₁ ， AB的中点．
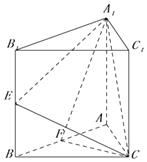
（I）已知M为线段B₁A₁上的点，且B₁A₁=4B₁M，求证：EM∥面A₁FC；
（II）若二面角E﹣A₁C﹣F所成角的余弦值为 $\text{[math]}$ ，求AA₁的值．

答案解析收藏纠错 + 选题
20. (2017·淮北模拟) 已知椭圆C₁： $\text{[math]}$ =1（a＞b＞0）的离心率e= $\text{[math]}$ ，且过点 $\text{[math]}$ ，直线l₁：y=kx+m（m＞0）与圆C₂：（x﹣1）²+y²=1相切且与椭圆C₁交于A，B两点．
（Ⅰ）求椭圆C₁的方程；
（Ⅱ）过原点O作l₁的平行线l₂交椭圆于C，D两点，设|AB|=λ|CD|，求λ的最小值．

答案解析收藏纠错 + 选题
21. (2017·淮北模拟) 已知函数发f（x）=（x+1）lnx﹣ax+2．
1. （1）当a=1时，求在x=1处的切线方程；
2. （2）若函数f（x）在定义域上具有单调性，求实数a的取值范围；
3. （3）求证： $\text{[math]}$ ，n∈N^* ．
答案解析收藏纠错 + 选题

四、选做题

22. (2017·淮北模拟) 以平面直角坐标系的原点为极点，以x轴的正半轴为极轴建立极坐标系．设曲线C的参数方程为 $\text{[math]}$ （α是参数），直线l的极坐标方程为ρcos（θ+ $\text{[math]}$ ）=2 $\text{[math]}$ ．
1. （1）求直线l的直角坐标方程和曲线C的普通方程；
2. （2）设点P为曲线C上任意一点，求点P到直线l的距离的最大值．
答案解析收藏纠错 + 选题
23. (2017·淮北模拟) 已知函数f（x）=|x+a|+|x﹣2|
1. （1）当a=﹣3时，求不等式f（x）≥3的解集；
2. （2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2017年安徽省淮北市高考数学一模试卷（理科）

副标题：

*注意事项：

2017年安徽省淮北市高考数学一模试卷（理科）

试题分析

总体分析

题量分析

难度分析

知识点分析

	与教育有关	与教育无关	合计
男	30	10	40
女	35	5	40
合计	65	15	80

P（K²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.023	6.635