江苏省如皋初级中学2019届九年级上学期数学期中考试试卷

更新时间：2019-01-07 浏览次数：392 类型：期中考试

一、单选题

1. (2018九上·江苏期中) 如图，⊙O的弦AB=16，OM⊥AB于M，且OM=6，则⊙O的半径等于（）

A . 8 B . 6 C . 10 D . 20

答案解析收藏纠错 + 选题
2. (2018九上·江苏期中) 若反比例函数 $\text{[math]}$ 的图象在每一象限内， y随x的增大而增大，则m的取值范围是（）

A . m<-4 B . m<0 C . m>-4 D . m>0

答案解析收藏纠错 + 选题
3. (2024九上·陆河期中) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . （﹣1，2） B . （﹣1，﹣2） C . （1，﹣2） D . （1，2）

答案解析收藏纠错 + 选题
4. (2018九上·江苏期中) 如图，A、B、C三点在⊙O上，且∠ACB＝40°，则∠AOB等于（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2018九上·江苏期中) 已知点M (－2，6)在双曲线 $\text{[math]}$ 上，则下列各点一定在该双曲线上的是（）

A . (2， 6) B . (－6，－2 ) C . (6，2) D . (2，－6)

答案解析收藏纠错 + 选题
6. (2018九上·江苏期中) 如图是二次函数 $\text{[math]}$ 的部分图象，由图象可知不等式 $\text{[math]}$ 的解集是（）

A . B . C . 且 D . x＜－1或x＞5

答案解析收藏纠错 + 选题
7. (2021九上·古浪月考) 圆心角为120°，弧长为12π的扇形半径为（　　）

A . 6 B . 9 C . 18 D . 36

答案解析收藏纠错 + 选题
8. (2020九上·全椒期末) 如图，二次函数 $\text{[math]}$ 的最大值为3，一元二次方程 $\text{[math]}$ 有实数根，则 $\text{[math]}$ 的取值范围是（）

A . m≥3 B . m≥-3 C . m≤3 D . m≤-3

答案解析收藏纠错 + 选题
9. (2019·重庆模拟) 如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C₁ ，它与x轴交于两点O，A₁；将C₁绕A₁旋转180°得到C₂ ，交x轴于A₂；将C₂绕A₂旋转180°得到C₃ ，交x轴于A₃；…如此进行下去，直至得到C₂₀₁₈ ，若点P（4035，m）在第2018段抛物线C₂₀₁₈上，则m的值是（）

A . 1 B . －1 C . 0 D . 4035

答案解析收藏纠错 + 选题
10. (2018九上·江苏期中) 如图，⊙O是以原点为圆心， $\text{[math]}$ 为半径的圆，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一点，过点 $\text{[math]}$ 作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（）

A . 3 B . 4 C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·江苏期中) 如图，AB是半圆的直径，点C、D是半圆上两点，∠ADC = 144°，则∠ABC = $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2018九上·江苏期中) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴有且只有一个公共点，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2018九上·江苏期中) 已知圆锥的底面直径为6cm，母线长为10cm，则此圆锥的侧面积为cm² ．

答案解析收藏纠错 + 选题
14. (2018九上·江苏期中) 校运动会小明参加铅球比赛，若某次投掷，铅球飞行的高度y（米）与水平距离x（米）之间的函数关系式为 $\text{[math]}$ ，那么小明这次投掷的成绩是米．

答案解析收藏纠错 + 选题
15. (2018九上·江苏期中) 如图，已知P、Q分别是⊙O的内接正六边形ABCDEF的边AB、BC上的点，AP=BQ，则∠POQ的度数为°．

答案解析收藏纠错 + 选题
16. (2018九上·江苏期中) 如图，点P在y轴正半轴上运动，点C在x轴上运动，过点P且平行于x轴的直线分别交函数 $\text{[math]}$ 和 $\text{[math]}$ 于A、B两点，则△ABC的面积等于．

答案解析收藏纠错 + 选题
17. (2018九上·江苏期中) 如图，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，连结AC，BD．若图中阴影部分的面积是 $\text{[math]}$ ，OA=2，则OC的长为．

答案解析收藏纠错 + 选题
18. (2018九上·江苏期中) 如图，过点C（2，1）分别作x轴、y轴的平行线，交直线y=﹣x+4于B、A两点，若二次函数y=ax²+bx+c的图象经过坐标原点O，且顶点在矩形ADBC内（包括边上），则a的取值范围是．

答案解析收藏纠错 + 选题

三、解答题

19. (2018九上·根河月考) 如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，完成下列问题：
1. （1）在图中标出圆心D，则圆心D点的坐标为；
2. （2）连接AD、CD，则∠ADC的度数为；
3. （3）若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面半径．
答案解析收藏纠错 + 选题
20. (2021九上·肃州期末) 如图，抛物线与直线y=x+3分别交于x轴和y轴上同一点，交点分别是点A和点C，且抛物线的对称轴为x=﹣2．
1. （1）求出抛物线与x轴的两个交点A、B的坐标．
2. （2）求出该抛物线的解析式．
答案解析收藏纠错 + 选题
21. (2018九上·江苏期中) 已知A(n，－2)，B(1，4)是一次函数y＝kx＋b的图象和反比例函数y＝ $\text{[math]}$ 的图象的两个交点，直线AB与y轴交于点C．
1. （1）求反比例函数和一次函数的关系式；
2. （2）求△AOC的面积；
3. （3）结合图象直接写出不等式kx＋b< $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
22. (2018九上·江苏期中) 如图，在▱ABCD中，AD=6，AB=10，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE．
1. （1）求弧DE的长；
2. （2）求阴影部分的面积．
答案解析收藏纠错 + 选题
23. (2018九上·江苏期中) 如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，点B是⊙O 上一点，AB是⊙O的切线，连接BP并延长，交直线l于点C．
1. （1）求证AB＝AC；
2. （2）若PC＝ $\text{[math]}$ ，OA＝15，求⊙O的半径的长．
答案解析收藏纠错 + 选题
24. (2018九上·江苏期中) 如图，在平面直角坐标系中，已知四边形ABCD为菱形，且A（0，3）、B（﹣4，0）．
1. （1）求经过点C的反比例函数的解析式；
2. （2）设P是（1）中所求函数图象上一点，以P、O、A顶点的三角形的面积与△COD的面积相等．求点P的坐标．
答案解析收藏纠错 + 选题
25. (2022九上·浦江期中) 如图，在平面直角坐标系xOy中，点O为坐标原点，正方形OABC的边OA，OC分别在x轴，y轴上，点B的坐标为（4，4），反比例函数 $\text{[math]}$ 的图象经过线段BC的中点D，交正方形OABC的另一边AB于点E．
1. （1）求k的值；
2. （2）如图①，若点P是x轴上的动点，连接PE，PD，DE，当△DEP的周长最短时，求点P的坐标；
3. （3）如图②，若点Q（x，y）在该反比例函数图象上运动（不与D重合），过点Q作QM⊥y轴，垂足为M，作QN⊥BC所在直线，垂足为N，记四边形CMQN的面积为S，求S关于x的函数关系式，并写出x的取值范围．
答案解析收藏纠错 + 选题
26. (2018九上·江苏期中) 某大学生利用暑假40天社会实践参与了一家网店经营，了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示．

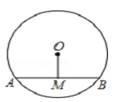
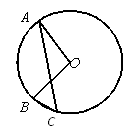
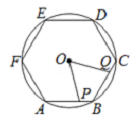
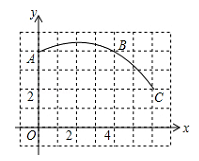
销售量p（件）

P=50—x

销售单价q（元/件）

当1≤x≤20时，q=30+ $\text{[math]}$ x；

当21≤x≤40时，q=20+ $\text{[math]}$
1. （1）求该网店第x天获得的利润y关于x的函数关系式；
2. （2）这40天中该网店第几天获得的利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
27. (2018九上·江苏期中) 如图，点P是反比例函数 $\text{[math]}$ 上第一象限上一个动点，点A、点B为坐标轴上的点，A（0，k），B（k，0）．已知△OAB的面积为 $\text{[math]}$ ．
1. （1）求k的值；
2. （2）连接PA、PB、AB，设△PAB的面积为S，点P的横坐标为t．请直接写出S与t的函数关系式；
3. （3）阅读下面的材料回答问题：
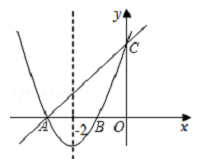
  当a＞0时， $\text{[math]}$
  
  ∵ $\text{[math]}$ ≥0，∴ $\text{[math]}$ ≥2，即 $\text{[math]}$ ≥2
  
  由此可知：当 $\text{[math]}$ =0时，即a=1时， $\text{[math]}$ 取得最小值2．
  
  问题：请你根据上述材料探索（2）中△PAB的面积S有没有最小值？若有，请直接写出S的最小值；若没有，说明理由．
答案解析收藏纠错 + 选题
28. (2018九上·江苏期中) 在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：
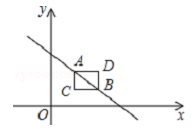
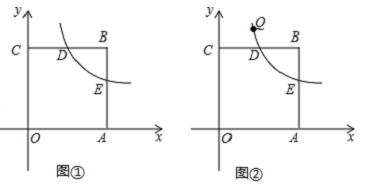
若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的外延矩形．点A，B，C的所有外延矩形中，面积最小的矩形称为点A，B，C的最佳外延矩形．例如，图中的矩形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都是点A，B，C的外延矩形，矩形 $\text{[math]}$ 是点A，B，C的最佳外延矩形．
1. （1）如图1，已知A（－2，0），B（4，3），C（0， $\text{[math]}$ ）．
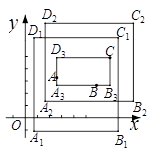
  ①若 $\text{[math]}$ ，则点A，B，C的最佳外延矩形的面积为；
  
  ②若点A，B，C的最佳外延矩形的面积为24，则的值为；
2. （2）如图2，已知点M（6，0），N（0，8）．P（ $\text{[math]}$ ， $\text{[math]}$ ）是抛物线 $\text{[math]}$ 上一点，求点M，N，P的最佳外延矩形面积的最小值，以及此时点P的横坐标的取值范围；
3. （3）如图3，已知点D（1，1）．E（ $\text{[math]}$ ， $\text{[math]}$ ）是函数 $\text{[math]}$ 的图象上一点，矩形OFEG是点O，D，E的一个面积最小的最佳外延矩形，⊙H是矩形OFEG的外接圆，请直接写出⊙H的半径r的取值范围．
答案解析收藏纠错 + 选题