2017年广东省深圳市高考数学一模试卷（理科）

更新时间：2017-04-06 浏览次数：835 类型：高考模拟

一、选择题：

1. (2017·深圳模拟) 若集合A={2，4，6，8}，B={x|x²﹣9x+18≤0}，则A∩B=（）

A . {2，4} B . {4，6} C . {6，8} D . {2，8}

答案解析收藏纠错 + 选题
2. (2017·深圳模拟) 若复数 $\text{[math]}$ （a∈R）为纯虚数，其中i为虚数单位，则a=（）

A . 2 B . 3 C . ﹣2 D . ﹣3

答案解析收藏纠错 + 选题
3. (2017·深圳模拟) 袋中装有大小相同的四个球，四个球上分别标有数字“2”，“3”，“4”，“6”，现从中随机选取三个球，则所选的三个球上的数字能构成等差数列的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2017·桂林模拟) 等比数列{a_n}的前n项和为S_n=a•3ⁿ^﹣¹+b，则 $\text{[math]}$ =（）

A . ﹣3 B . ﹣1 C . 1 D . 3

答案解析收藏纠错 + 选题
5. (2017·银川模拟) 直线l：kx+y+4=0（k∈R）是圆C：x²+y²+4x﹣4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
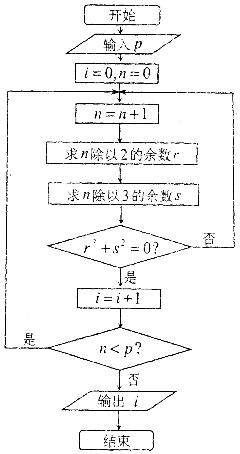
6. (2017·深圳模拟) 祖冲之之子祖暅是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等．此即祖暅原理．利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为h（0＜h＜2）的平面截该几何体，则截面面积为（）

A . 4π B . πh² C . π（2﹣h）² D . π（4﹣h）²

答案解析收藏纠错 + 选题
7. (2017·深圳模拟) 函数f（x）= $\text{[math]}$ •cosx的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2017·深圳模拟) 已知a＞b＞0，c＜0，下列不等关系中正确的是（）

A . ac＞bc B . a^c＞b^c C . log_a（a﹣c）＞log_b（b﹣c） D . $\text{[math]}$ ＞ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017·深圳模拟) 执行如图所示的程序框图，若输入p=2017，则输出i的值为（）

A . 335 B . 336 C . 337 D . 338

答案解析收藏纠错 + 选题
10. (2017·葫芦岛模拟) 已知F是双曲线E： $\text{[math]}$ =1（a＞0，b＞0）的右焦点，过点F作E的一条渐近线的垂线，垂足为P，线段PF与E相交于点Q，记点Q到E的两条渐近线的距离之积为d² ，若|FP|=2d，则该双曲线的离心率是（）

A . $\text{[math]}$ B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
11. (2017·深圳模拟) 已知棱长为2的正方体ABCD﹣A₁B₁C₁D₁ ，球O与该正方体的各个面相切，则平面ACB₁截此球所得的截面的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2017·深圳模拟) 已知函数f（x）= $\text{[math]}$ ，x≠0，e为自然对数的底数，关于x的方程 $\text{[math]}$ + $\text{[math]}$ ﹣λ=0有四个相异实根，则实数λ的取值范围是（）

A . （0， $\text{[math]}$ ） B . （2 $\text{[math]}$ ，+∞） C . （e+ $\text{[math]}$ ，+∞） D . （ $\text{[math]}$ + $\text{[math]}$ ，+∞）

答案解析收藏纠错 + 选题

二、填空题：

13. (2017·深圳模拟) 已知向量 $\text{[math]}$ =（1，2）， $\text{[math]}$ =（x，3），若 $\text{[math]}$ ⊥ $\text{[math]}$ ，则| $\text{[math]}$ + $\text{[math]}$ |=．

答案解析收藏纠错 + 选题
14. (2017·深圳模拟) （ $\text{[math]}$ ﹣ $\text{[math]}$ ）⁵的二项展开式中，含x的一次项的系数为（用数字作答）．

答案解析收藏纠错 + 选题
15. (2017·深圳模拟) 若实数x，y满足不等式组 $\text{[math]}$ ，目标函数z=kx﹣y的最大值为12，最小值为0，则实数k=．

答案解析收藏纠错 + 选题
16. (2017·深圳模拟) 已知数列{a_n}满足na_n₊₂﹣（n+2）a_n=λ（n²+2n），其中a₁=1，a₂=2，若a_n＜a_n₊₁对∀n∈N^*恒成立，则实数λ的取值范围是．

答案解析收藏纠错 + 选题

三、解答题：

17. (2017·深圳模拟) △ABC的内角A、B、C的对边分别为a、b、c，已知2a= $\text{[math]}$ csinA﹣acosC．
1. （1）求C；
2. （2）若c= $\text{[math]}$ ，求△ABC的面积S的最大值．
答案解析收藏纠错 + 选题
18. (2017·深圳模拟) 如图，四边形ABCD为菱形，四边形ACEF为平行四边形，设BD与AC相交于点G，AB=BD=2，AE= $\text{[math]}$ ，∠EAD=∠EAB．
1. （1）证明：平面ACEF⊥平面ABCD；
2. （2）若AE与平面ABCD所成角为60°，求二面角B﹣EF﹣D的余弦值．
答案解析收藏纠错 + 选题
19. (2017·深圳模拟) 某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费．
1. （1）求某户居民用电费用y（单位：元）关于月用电量x（单位：度）的函数解析式；
2. （2）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的点80%，求a，b的值；
3. （3）在满足（2）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点值代替，记Y为该居民用户1月份的用电费用，求Y的分布列和数学期望．
答案解析收藏纠错 + 选题
20. (2017·深圳模拟) 已成椭圆C： $\text{[math]}$ =1（a＞b＞0）的左右顶点分别为A₁、A₂ ，上下顶点分别为B₂/B₁ ，左右焦点分别为F₁、F₂ ，其中长轴长为4，且圆O：x²+y²= $\text{[math]}$ 为菱形A₁B₁A₂B₂的内切圆．
1. （1）求椭圆C的方程；
2. （2）点N（n，0）为x轴正半轴上一点，过点N作椭圆C的切线l，记右焦点F₂在l上的射影为H，若△F₁HN的面积不小于 $\text{[math]}$ n² ，求n的取值范围．
答案解析收藏纠错 + 选题
21. (2017·深圳模拟) 已知函数f（x）=xlnx，e为自然对数的底数．
1. （1）求曲线y=f（x）在x=e^﹣²处的切线方程；
2. （2）关于x的不等式f（x）≥λ（x﹣1）在（0，+∞）上恒成立，求实数λ的值；
3. （3）关于x的方程f（x）=a有两个实根x₁ ， x₂ ，求证：|x₁﹣x₂|＜2a+1+e^﹣² ．
答案解析收藏纠错 + 选题
22. (2017·深圳模拟) 在直角坐标系中xOy中，已知曲线E经过点P（1， $\text{[math]}$ ），其参数方程为 $\text{[math]}$ （α为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系．
1. （1）求曲线E的极坐标方程；
2. （2）若直线l交E于点A、B，且OA⊥OB，求证： $\text{[math]}$ 为定值，并求出这个定值．
答案解析收藏纠错 + 选题
23. (2017·衡阳模拟) 已知f（x）=|x+a|，g（x）=|x+3|﹣x，记关于x的不等式f（x）＜g（x）的解集为M．
1. （1）若a﹣3∈M，求实数a的取值范围；
2. （2）若[﹣1，1]⊆M，求实数a的取值范围．
答案解析收藏纠错 + 选题