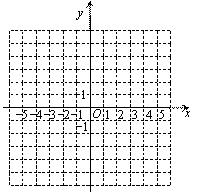
B .
B .  C .
C . 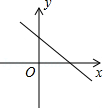 D .
D . 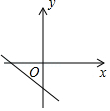

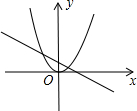 B .
B . 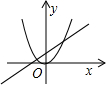 C .
C . 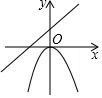 D .
D . 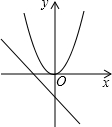
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则 ②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )