2018-2019学年初中数学北师大版九年级下册2.5二次函...

更新时间：2019-03-13 浏览次数：339 类型：同步测试

一、单选题

1. (2019九上·杭州月考) 抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点坐标是（）

A . (0， 1) B . (1， 0) C . (0， -1) D . (0， 0)

答案解析收藏纠错 + 选题
2. (2021九上·合肥月考) 如图为抛物线y=ax²+bx+c的图象，A，B，C为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（）

A . a+b=﹣1 B . a﹣b=﹣1 C . b＜2a D . ac＜0

答案解析收藏纠错 + 选题
3. 二次函数y=ax²+bx+c（a≠0）的函数值y与自变量x的四组对应值如表所示

x

6.15

6.18

6.21

6.24

y

0.02

-0.01

0.02

0.11

则方程ax²+bx+c=0的根的个数是（）

A . 0 B . 1 C . 2 D . 不能确定

答案解析收藏纠错 + 选题
4. 小兰画了一个函数y=x²+ax+b的图象如图，则关于x的方程x²+ax+b=0的解是（）

A . 无解 B . x=1 C . x=﹣4 D . x=﹣1或x=4

答案解析收藏纠错 + 选题
5. 已知抛物线y=x²﹣x﹣1与x轴的一个交点为（m，0），则代数式m²﹣m+2014的值为（）

A . 2012 B . 2013 C . 2014 D . 2015

答案解析收藏纠错 + 选题
6. (2018九上·仙桃期中) 如图，抛物线 $\text{[math]}$ 与x轴交于点A、B，把抛物线在x轴及其下方的部分记作 $\text{[math]}$ ，将 $\text{[math]}$ 向左平移得到 $\text{[math]}$ ， $\text{[math]}$ 与x轴交于点B、D，若直线 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 共有3个不同的交点，则m的取值范围是 $\text{[math]}$ $\text{[math]}$

A . B . C . D .

答案解析收藏纠错 + 选题
7. 下列关于二次函数y＝ax²－2ax+1（a＞1）的图象与x轴交点的判断，下确的是（）

A . 没有交点 B . 只有一个交点，且它位于y轴右侧 C . 有两个交点，且它们均位于y轴左侧 D . 有两个交点，且它们均位于y轴右侧

答案解析收藏纠错 + 选题
8. 二次函数y=x²+2x﹣m²+1的图像与直线y=1的公共点个数是（）

A . 0 B . 1 C . 2 D . 1或2

答案解析收藏纠错 + 选题
9. 根据抛物线y＝x²＋3x－1与x轴的交点的坐标，可以求出下列方程中哪个方程的近似解（）

A . x²＋3x－1＝0 B . x²＋3x＋1＝0 C . 3x²＋x－1＝0 D . x²－3x＋1＝0

答案解析收藏纠错 + 选题
10. (2020·上饶模拟) “如果二次函数y=ax²+bx+c的图象与x轴有两个公共点，那么一元二次方程ax²+bx+c=0有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m、n（m＜n）是关于x的方程1﹣（x﹣a）（x﹣b）=0的两根，且a＜b，则a、b、m、n的大小关系是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·绍兴月考) 二次函数 $\text{[math]}$ 与两坐标轴的三个交点确定的三角形的面积是．

答案解析收藏纠错 + 选题
12. (2018九上·湖州期中) 如图，已知抛物线y=x²+bx+c经过点(0，－3)，请你确定一个b的值，使该抛物线与x轴的一个交点在(1，0)和(3，0)之间．你所确定的b的值是．

答案解析收藏纠错 + 选题
13. (2018九上·宁波期中) 若抛物线y=2 $\text{[math]}$ +x+c与坐标轴有两个交点，则字母c应满足的条件是．

答案解析收藏纠错 + 选题
14. (2023九上·新余月考) 若函数 $\text{[math]}$ 的图像与x轴有且只有一个交点，则a的值为 .

答案解析收藏纠错 + 选题
15. (2023九上·阿克苏月考) 二次函数y=ax²+bx+c的图象如图所示，则方程ax²+bx+c=0的两根为．

答案解析收藏纠错 + 选题
16. 二次函数y＝x²＋ax＋a与x轴的交点分别是A(x₁ ， 0)、B(x₂ ， 0)，且x₁＋x₂－x₁x₂＝－10，则抛物线的顶点坐标是．

答案解析收藏纠错 + 选题

三、解答题

17. 如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，交y轴于点C，点D为抛物线的顶点，连接BD，点H为BD的中点．请解答下列问题：
1. （1）求抛物线的解析式及顶点D的坐标；
2. （2）在y轴上找一点P，使PD+PH的值最小，则PD+PH的最小值为．
  （注：抛物线y=ax²+bx+c（a≠0）的对称轴是直线x=﹣ $\text{[math]}$ ，顶点坐标为（﹣ $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
18. 如图，二次函数y=ax²+bx+c的图象经过A、B、C三点．
1. （1）观察图象，写出A、B、C三点的坐标，并求出抛物线解析式；
2. （2）求此抛物线的顶点坐标和对称轴；
3. （3）当m取何值时，ax²+bx+c=m有两个不相等的实数根．
答案解析收藏纠错 + 选题
19. (2018九上·南昌期中) 已知一元二次方程x²+x﹣2=0有两个不相等的实数根，即x₁=1，x₂=﹣2．
1. （1）求二次函数y=x²+x﹣2与x轴的交点坐标；
2. （2）若二次函数y=﹣x²+x+a与x轴有一个交点，求a的值．
答案解析收藏纠错 + 选题
20. (2018九上·三门期中) 已知：二次函数y=﹣2x²+4x+m+1，与x轴的公共点为A，B．
1. （1）如果A与B重合，求m的值；
2. （2）横、纵坐标都是整数的点叫做整点：
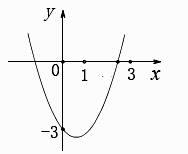
  ①当m=﹣1时，求线段AB上整点的个数；
  
  ②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n≤8时，结合函数的图象，求m的取值范围．
答案解析收藏纠错 + 选题
21. (2018九上·宁波期中) 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)²-4，AB为半圆的直径，求这个“果圆”被y轴截得的CD的长．

答案解析收藏纠错 + 选题
22. (2019九上·交城期中) 已知二次函数 $\text{[math]}$ （ $\text{[math]}$ 为常数）.
1. （1）求证：不论 $\text{[math]}$ 为何值，该函数的图象与 $\text{[math]}$ 轴总有公共点；
2. （2）当 $\text{[math]}$ 取什么值时，该函数的图象与 $\text{[math]}$ 轴的交点在 $\text{[math]}$ 轴的上方？
答案解析收藏纠错 + 选题
23. 根据下列要求，解答相关问题．
1. （1）请补全以下求不等式 $\text{[math]}$ 的解集的过程：
  ①构造函数，画出图象：根据不等式特征构造二次函数y= $\text{[math]}$ ；并在下面的坐标系中（图1）画出二次函数y= $\text{[math]}$ 的图象（只画出大致图象即可）；
  ②求得界点，标示所需：当 $\text{[math]}$ 时，求得方程 $\text{[math]}$ 的解为；并用虚线标示出函数y= $\text{[math]}$ 图象中 $\text{[math]}$ ＜0的部分；
  ③借助图象，写出解集：由所标示图象，可得不等式 $\text{[math]}$ ＜0的解集为．
2. （2）请你利用上面求不等式解集的过程，求不等式 $\text{[math]}$ -3≥0的解集．
答案解析收藏纠错 + 选题
24. 某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上．在乒乓球运行时，设乒乓球与端点A的水平距离为x（米），与桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：
t（秒）
0
0.16
0.2
0.4
0.6
0.64
0.8
6
X（米）
0
0.4
0.5
1
1.5
1.6
2
…
y（米）
0.25
0.378
0.4
0.45
0.4
0.378
0.25
…
1. （1）当t为何值时，乒乓球达到最大高度？
2. （2）乒乓球落在桌面时，与端点A的水平距离是多少？
3. （3）乒乓球落在桌面上弹起后，y与x满足y=a（x﹣3）²+k．
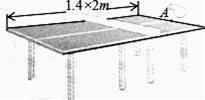
  ①用含a的代数式表示k；
  ②球网高度为0.14米，球桌长（1.4×2）米．若球弹起后，恰好有唯一的击球点，可以将球沿直线扣杀到点A，求a的值．
答案解析收藏纠错 + 选题