
甲:1.以点C为圆心,AB长为半径画弧;2.以点A为圆心,BC长为半径画弧;3.两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1).
乙:1.连接AC,作线段AC的垂直平分线,交AC于点M;2.连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )
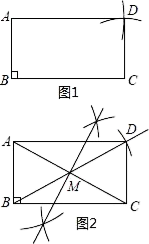



要求:(1)图①中的△APC为直角三角形,图②中的△APC为锐角三角形.(2)只用无刻度的直尺,保留适当的作图痕迹.

【收集数据】甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
按如下分数段整理、描述这两组样本数据
|
组别 班级 |
65.6~70.5 |
70.5~75.5 |
75.5~80.5 |
80.5~85.5 |
85.5~90.5 |
90.5~95.5 |
|
甲班 |
2 |
2 |
4 |
5 |
1 |
1 |
|
乙班 |
1 |
1 |
a |
b |
2 |
0 |
在表中,a=,b=.
|
班级 |
平均数 |
众数 |
中位数 |
方差 |
|
甲班 |
80 |
x |
80 |
47.6 |
|
乙班 |
80 |
80 |
y |
26.2 |
在表中:x=,y=.
②若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类相关知识合格的学生有人
③你认为哪个班的学生掌握垃圾分类相关知识的情况较好,说明理由.

如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是.
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由.
如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是边AB上一点,当∠DCE=45°,BE=2时,则DE的长为.

①求m的值;
②点P是x轴负半轴上一点,设抛物线L1、L2的“共点”为Q,作点P关于点Q的对称点P′,以PP′为对角线作正方形PMP′N,当点M或点N落在抛物线L1上时,直接写出点P的坐标.