 B .
B .  C .
C .  D .
D . 

| X | …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| Y | …… | 3 | 0 | ﹣1 | 0 | 3 |
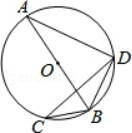
①物线y=ax2+bx+c的开口向下;②抛物线y=ax2+bx+c的对称轴为直线x=﹣1;③方程ax2+bx+c=0的根为0和2;④当y>0时,x的取值范围是x<0或x>2以上结论中其中的是( )
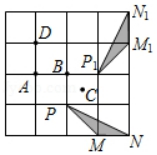
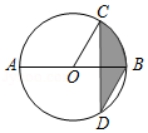
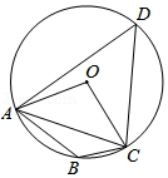
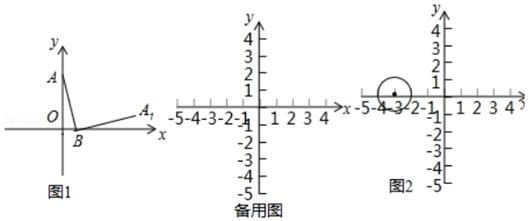
B、DC于点M、N . 动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x , 圆心O与P点的距离为y , 图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )


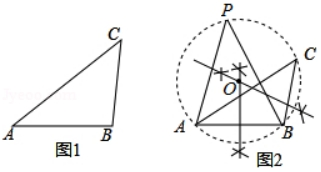
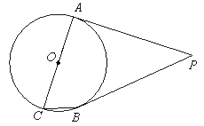
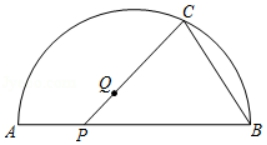
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB .
小明的做法如下:
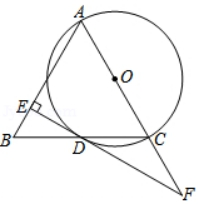
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n , 与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P , 连结AP , BP .
所以∠APB=∠ACB .
老师说:“小明的作法正确.”
请回答:

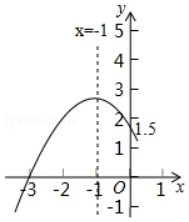

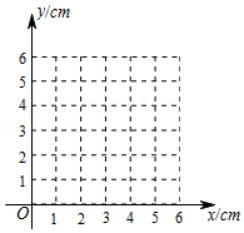
小明根据学习函数的经验,分别对函数y1 , y2 , 随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
|
x/cm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y1/cm |
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
y2/cm |
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
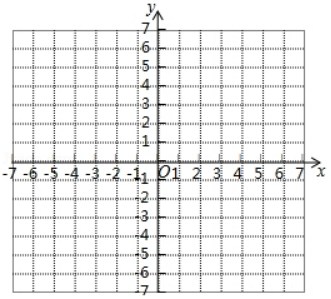
①若在抛物线上存在点P , 使得∠POQ=45°,求点P的坐标.
②抛物线与直线y=1交于点E , F(点E在点F的左侧),将此抛物线在点E , F(包含点E和点F)之间的部分沿x轴向左平移n个单位后得到的图象记为G , 若在图象G上存在点P , 使得∠POQ=45°,求n的取值范围.
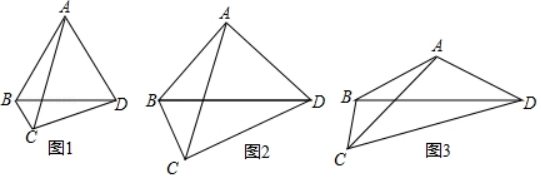
①当点B的坐标分别为(1,0),(﹣2,0)时,点A关于点B的“伴随点”的坐标分别为,;