江苏省扬州市邵樊片2019-2020学年八年级上学期数学10...

更新时间：2019-11-27 浏览次数：325 类型：月考试卷

一、单选题

1. (2019八上·灌云月考) 下列图形中是轴对称的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·赵县期末) 如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线，这条射线就是角的平分线，在这个操作过程中，运用了三角形全等的判定方法是（）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
3. (2023八上·涿州月考) 如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）

A . 150° B . 180° C . 210° D . 225°

答案解析收藏纠错 + 选题
4. (2022八上·诸城期中) 三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019八上·扬州月考) 如图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（）

A . 点A B . 点B C . 点C D . 点D

答案解析收藏纠错 + 选题
6. (2019八上·扬州月考) 如图所示，将一个正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“ ”的图形，将纸片展开，得到的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2019八上·扬州月考) 一个等腰三角形的三边长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ,该等腰三角形的周长是（）

A . 10或4 B . 10或7 C . 4或7 D . 10或4或7

答案解析收藏纠错 + 选题
8. (2022八上·杭州期中) 如图，在△ABC中，∠B＞90°，CD为∠ACB的角平分线，在AC边上取点E，使DE＝DB，且∠AED＞90°.若∠A＝α，∠ACB＝β，则（）

A . ∠AED＝180°﹣α﹣β B . ∠AED＝180°﹣α﹣ $\text{[math]}$ β C . ∠AED＝90°﹣α+β D . ∠AED＝90°+α+ $\text{[math]}$ β

答案解析收藏纠错 + 选题

二、填空题

9. (2021八上·宜州期中) 一个等腰三角形的两边长分别是1m和2m，则它的周长是m.

答案解析收藏纠错 + 选题
10. (2020八上·青白江期末) 已知等腰三角形的一个内角是80°，则它的底角是

答案解析收藏纠错 + 选题
11. (2019九下·东台月考) 如下图，在Rt△ABC中，∠C=90°，DE垂直平分AB，垂足为E，D在BC上，已知∠CAD=32°，则∠B=度．

答案解析收藏纠错 + 选题
12. (2020八上·阜宁月考) 如图，等边△ABC中，AD是中线，AD=AE，则∠EDC=

答案解析收藏纠错 + 选题
13. (2019八上·扬州月考) 如图，等边三角形ABC的边长为2cm，D、E分别是为AB、AC上的点，将四边形DBCE沿直线DE折叠，点B、C分别落在B′、C′处，且都在△ABC的外部，则阴影部分图形的周长为cm.

答案解析收藏纠错 + 选题
14. (2019八上·扬州月考) 如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C.若P是BC边上一动点，则DP长的最小值为。

答案解析收藏纠错 + 选题
15. (2019八上·扬州月考) 如图，∠BAC＝θ（0°＜θ＜90°），现只用4根等长的小棒将∠BAC固定，从点A₁开始依次向右摆放，其中A₁A₂为第1根小棒，且A₁A₂＝AA₁ ，则角θ的取值范围是.

答案解析收藏纠错 + 选题
16. (2019八上·扬州月考) 如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM.下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC.其中正确的是

答案解析收藏纠错 + 选题

三、解答题

17. (2019八上·扬州月考) 如图，在相同小正方形组成的网格纸上，有三个黑色方块，请你用三种不同的方法分别在图①、图②、图③上再选一个小正方形方块涂黑，使得四个黑色方块组成轴对称图形.

答案解析收藏纠错 + 选题
18. (2019八上·扬州月考) 如图
1. （1）如图1，利用网格线，作出三角形关于直线l的对称图形.
2. （2）如图2，利用网格线：
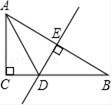
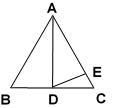
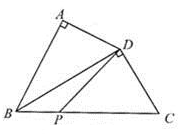
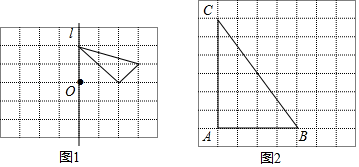
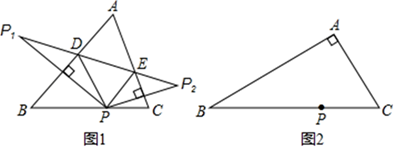
  ①在BC上找一点P，使点P到AB和AC的距离相等；
  
  ②在射线AP上找一点Q，使QB＝QC.写出此时QB与QC的位置关系.
答案解析收藏纠错 + 选题
19. (2019八上·扬州月考) 如图，AB＝CD，EC＝BF，∠ECA＝∠DBF，AC＝6，BC＝4.
1. （1）求证：AE∥DF；
2. （2）求AD的长度.
答案解析收藏纠错 + 选题
20. (2021八上·固原月考) 如图，给出五个等量关系：①AD＝BC；②AC＝BD；③CE＝DE；④∠D＝∠C；⑤∠DAB＝∠CBA.

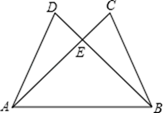
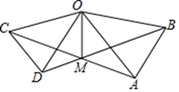
请你以其中两个为条件，另外三个中的一个为结论，推出一个正确的结论（只需写出一种情况），并加以证明.

已知：

求证：

证明：

答案解析收藏纠错 + 选题
21. (2019七下·张店期末) 如图，在三角形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边的垂直平分线，且分别交 $\text{[math]}$ 于点 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ 是等边三角形.

答案解析收藏纠错 + 选题
22. (2019八上·扬州月考) 在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，
1. （1）求证：Rt△ABE≌Rt△CBF；
2. （2）若∠CAE=30°，求∠ACF度数.
答案解析收藏纠错 + 选题
23. (2019七下·宽城期末) 用一条长为18cm的细绳围成一个等腰三角形.
1. （1）如果腰长是底边长的2倍，求三角形各边的长.
2. （2）能围成有一边的长是4cm的等腰三角形吗？若能，求出其他两边的长；若不能，请说明理由.
答案解析收藏纠错 + 选题
24. (2019八上·扬州月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，作AB边的垂直平分线交直线BC于M，交AB于点N.
1. （1）如图 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ =度；
2. （2）如图 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ =度；
3. （3）如图 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ =度；
4. （4）由 $\text{[math]}$ 问，你能发现 $\text{[math]}$ 与∠A有什么关系？写出猜想，并证明。
答案解析收藏纠错 + 选题
25. (2019八上·扬州月考) 如图，已知∠MON＝30°，点A₁、A₂、A₃……在射线ON上，点B₁、B₂、B₃……在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄……均为等边三角形，且OA₁＝1.
1. （1）分别求出△A₁B₁A₂、△A₃B₃A₄的边长；
2. （2）求△A₇B₇A₈的周长（直接写出结果）.
答案解析收藏纠错 + 选题
26. (2019八上·扬州月考) 如图1，在△ABC中，∠A＜90°，P是BC边上的一点，P₁ ， P₂是点P关于AB、AC的对称点，连结P₁P₂ ，分别交AB、AC于点D、E.
1. （1）若∠A＝52°，求∠DPE的度数；
2. （2）如图2，在△ABC中，若∠BAC＝90°，用三角板作出点P关于AB、AC的对称点P₁、P₂ ，（不写作法，保留作图痕迹），试判断点P₁ ， P₂与点A是否在同一直线上，并说明理由.
答案解析收藏纠错 + 选题
27. (2020八上·滨江期中) 如图1，直线AM⊥AN，AB平分∠MAN，过点B作BC⊥BA交AN于点C；动点E、D同时从A点出发，其中动点E以2cm/s的速度沿射线AN方向运动，动点D以1cm/s的速度运动；已知AC＝6cm，设动点D，E的运动时间为t.
1. （1）当点D在射线AM上运动时满足S_△_ADB：S_△_BEC＝2：1，试求点D，E的运动时间t的值；
2. （2）当动点D在直线AM上运动，E在射线AN运动过程中，是否存在某个时间t，使得△ADB与△BEC全等？若存在，请求出时间t的值；若不存在，请说出理由.
答案解析收藏纠错 + 选题
28. (2021八上·桐城期末) 如图，在△ABC中，BA=BC，D在边CB上，且DB=DA=AC.
1. （1）如图1，填空∠B=°，∠C=°；
2. （2）若M为线段BC上的点，过M作直线MH⊥AD于H，分别交直线AB、AC与点N、E，如图2
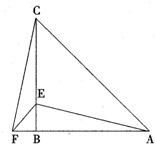
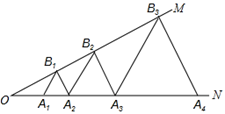
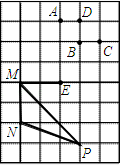
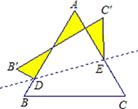
  ①求证：△ANE是等腰三角形；
  
  ②试写出线段BN、CE、CD之间的数量关系，并加以证明.
答案解析收藏纠错 + 选题