 B .
B .  C .
C .  D .
D . 
区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
则这10个区县该日最高气温的中位数是( ).
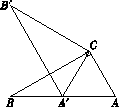
如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转 角(0°<
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则
等于( ).
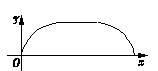 B .
B .  C .
C . 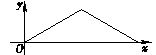 D .
D . 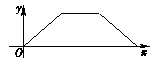
《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短.横之不出四尺,纵之不出二尺,斜之适出注.问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰 好能出去.解决下列问题:

表1 学农1班所抽取酸奶添加蔗糖克数统计表 (单位:克)
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
蔗糖质量 | 4.5 | 5.8 | 5.4 | 6.9 | 4.2 | 7 | 4.9 | 5.8 | 9.8 | 6.8 |
表2,学农2班所抽取酸奶添加蔗糖克数统计表(单位:克)
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
蔗糖质量 | 7.4 | 4.9 | 7.8 | 4.1 | 7.2 | 5.8 | 7.6 | 6.8 | 4.5 | 4.9 |
据研究发现,若蔗糖含量在5%~8%,即100克酸奶中,含糖5~8克的酸奶口感最佳.两班所抽取酸奶的相关统计数据如表3所示.
表3两班所抽取酸奶的统计数据表
酸奶口感最佳的杯数 (杯) | 每杯酸奶中添加的 蔗糖克数平均值(克) | 每杯酸奶中添加的 蔗糖克数的方差 | |
学农1班 | x | 6.11 | 2.39 |
学农2班 | 6 | 6.1 | 1.81 |
根据以上材料回答问题:
阅读以下内容并回答问题:

小雯用这个方法进行了尝试,点 向上平移3个单位后的对应点
的坐标为,过点
的直线的解析式为.
请你继续利用这个方法解决问题:
对于平面直角坐标系xOy内的图形M,将图形M上所有点都向上平移3个单位,再向右平移1个单位,我们把这个过程称为图形M的一次“斜平移”. 求将直线 进行两次“斜平移”后得到的直线的解析式.

先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
如图,在平面直角坐标系xOy中,点 在直线
上,过点
作
∥y轴,交直线
于点
,以
为直角顶点,
为直角边,在
的右侧作等腰直角三角形
;再过点
作
∥y轴,分别交直线
和
于
,
两点,以
为直角顶点,
为直角边,在
的右侧作等腰直角三角形
,…,按此规律进行下去,点
的横坐标为,点
的横坐标为,点
的横坐标为.(用含n的式子表示,n为正整数)

如图,

在由边长都为1个单位长度的小正方形组成的 正方形网格中,点A , B , P 都在格点上.请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:
条件1:点P到四边形的两个顶点的距离相等;
条件2:点P在四边形的内部或其边上;
条件3:四边形至少一组对边平行.
如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.

①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.