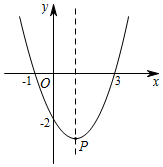
如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )

如图,A,B是半径为1的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到点A运动结束,设运动时间为x(单位:s),弦BP的长为y,那么下列图象中可能表示y与x函数关系的是( )
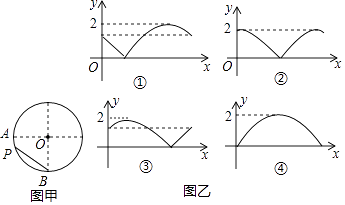
 B .
B .  C .
C .  D .
D . 



②△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
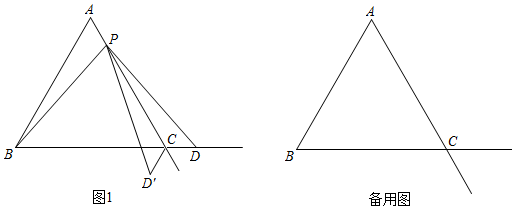
①求证:PB=PD;
②请求出∠BPD′的度数;
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
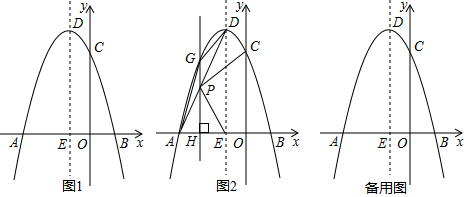
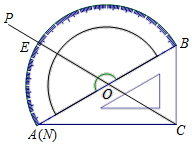
①求点P的坐标;
②连接PC、PE,探究PC、PE的数量关系和位置关系,并说明理由;