山西省吕梁市交城县2022-2023学年九年级上学期期中考试...

更新时间：2023-01-07 浏览次数：63 类型：期中考试

一、单选题

1. (2022九上·交城期中) 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A . 等边三角形 B . 正五角星 C . 正六边形 D . 平行四边形

答案解析收藏纠错 + 选题
2. (2022九上·交城期中) 一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
3. (2022九上·交城期中) 我们学习了一次函数、二次函数和反比例函数，回顾学习过程，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现的数学思想是（）

A . 演绎 B . 数形结合 C . 抽象 D . 公理化

答案解析收藏纠错 + 选题
4. (2022九上·交城期中) 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（）．

A . 60° B . 90° C . 120° D . 150°

答案解析收藏纠错 + 选题

5. (2022九上·交城期中) 二次函数 $\text{[math]}$ （a≠0）中x，y的部分对应值如下表：

x	…	-2	-1	0	1	2	…
y	…	0	-4	-6	-6	-4	…

则该二次函数图象的对称轴为（）

A . y轴 B . 直线x＝ $\text{[math]}$ C . 直线x＝1 D . 直线x＝ $\text{[math]}$

答案解析收藏纠错 + 选题

6. (2022九上·交城期中) 将抛物线 $\text{[math]}$ 向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·自贡模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·盐山月考) 有一个两位数，个位数字与十位数字之和为8，把它的个位数字与十位数字对调，得到一个新数，新数与原数之积为1855，则原两位数是（）

A . 35 B . 53 C . 62 D . 35或53

答案解析收藏纠错 + 选题
9. (2022九上·交城期中) 已知二次函数 $\text{[math]}$ 的图象过点A $\text{[math]}$ ， B $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·交城期中) 如图，二次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象与 $\text{[math]}$ 轴交于点A，B，且点A在 $\text{[math]}$ 和0之间，图象与 $\text{[math]}$ 轴交于负半轴，对称轴为直线 $\text{[math]}$ ，对于该二次函数，下列结论中错误的是（）

A . 二次函数的最小值为 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·交城期中) 抛物线 $\text{[math]}$ 的顶点坐标是.

答案解析收藏纠错 + 选题
12. (2022九上·交城期中) 在2020年太原五中秋季运动会上，某班参加圆周接力的同学每两人握一次手，共握手190次，设参加圆周接力的人数为x，则可列方程为.

答案解析收藏纠错 + 选题
13. (2022九上·交城期中) 飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是 $\text{[math]}$ ．则飞机着陆后滑行的最大距离是m．

答案解析收藏纠错 + 选题
14. (2022九上·交城期中) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ （ $\text{[math]}$ 为常数， $\text{[math]}$ ）的两根分别为 $\text{[math]}$ ， $\text{[math]}$ ，那么关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的两根分别为．

答案解析收藏纠错 + 选题
15. (2022九上·交城期中) 如图， $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积等于．

答案解析收藏纠错 + 选题

三、解答题

16. (2022九上·交城期中) 解下列方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2022九上·交城期中) 已知关于x的一元二次方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求k的取值范围；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，求实数k的值．
答案解析收藏纠错 + 选题
18. (2022九上·交城期中) 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：
⑴作出△ABC绕点A逆时针旋转90°的△AB₁C₁ ．
⑵作出△AB₁C₁关于原点O成中心对称的△A₁B₂C₂ ．
⑶请直接写出以A₁、B₂、C₂为顶点的平行四边形的第四个顶点D的坐标．

答案解析收藏纠错 + 选题
19. (2022九上·交城期中) 如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD＝CD，过点D作⊙O的切线交边AC于点F.
1. （1）求证：DF⊥AC；
2. （2）若⊙O的半径为5，∠CDF＝30°，求弧BD的长(结果保留π)．
答案解析收藏纠错 + 选题
20. (2022九上·交城期中) 阅读以下材料，并按要求完成相应的任务．
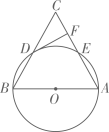
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？用现在的数学语言表达是：如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ 寸， $\text{[math]}$ 尺，其中1尺 $\text{[math]}$ 寸，求出直径 $\text{[math]}$ 的长．
解题过程如下：
连接 $\text{[math]}$ ，设 $\text{[math]}$ 寸，则 $\text{[math]}$ 寸．
∵ $\text{[math]}$ 尺，∴ $\text{[math]}$ 寸．
在 $\text{[math]}$ 中， $\text{[math]}$ ，即 $\text{[math]}$ ，解得 $\text{[math]}$ ，
∴ $\text{[math]}$ 寸．
任务：
1. （1）上述解题过程运用了定理和定理．
2. （2）若原题改为已知 $\text{[math]}$ 寸， $\text{[math]}$ 尺，请根据上述解题思路，求直径 $\text{[math]}$ 的长．
3. （3）若继续往下锯，当锯到 $\text{[math]}$ 时，弦 $\text{[math]}$ 所对圆周角的度数为．
答案解析收藏纠错 + 选题
21. (2022九上·交城期中) 某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元.市场调查发现，这种双肩包每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+60（30≤x≤60）.设这种双肩包每天的销售利润为w元.
1. （1）求w与x之间的函数关系式；
2. （2）这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
3. （3）如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少.
答案解析收藏纠错 + 选题
22. (2022九上·交城期中) 综合与实践
【情境呈现】如图1，将两个正方形纸片 $\text{[math]}$ 和 $\text{[math]}$ 放置在一起.若固定正方形 $\text{[math]}$ ，将正方形 $\text{[math]}$ 绕着点A旋转．
1. （1）【数学思考】如图1，当点E在 $\text{[math]}$ 边上，点G在 $\text{[math]}$ 边上时，线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是，位置关系是．
2. （2）如图2，是将正方形 $\text{[math]}$ 绕着点A逆时针旋转 $\text{[math]}$ 度得到的，则（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
3. （3）【拓展探究】如图3，若点D，E，G在同一条直线上，且 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长度（直接写出答案）．
答案解析收藏纠错 + 选题
23. (2022九上·交城期中) 如图，已知抛物线 $\text{[math]}$ $\text{[math]}$ 的顶点坐标为Q $\text{[math]}$ ，且与 $\text{[math]}$ 轴交C $\text{[math]}$ ，与 $\text{[math]}$ 轴交于A，B两点（点A在点B的右侧），点P是抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作 $\text{[math]}$ 直线 $\text{[math]}$ 于点D．
1. （1）求该抛物线的解析式及A，B两点的坐标；
2. （2）求点P在运动的过程中，线段PD的最大值；
3. （3）若点P与点Q重合，点E在 $\text{[math]}$ 轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题