浙江省温州市2020年数学中考模拟试卷

更新时间：2024-11-06 浏览次数：386 类型：中考模拟

一、选择题（共10小题）

1. (2020·温州模拟) 计算：﹣5+2的结果是（　　）

A . ﹣3 B . ﹣1 C . 1 D . 3

答案解析收藏纠错 + 选题
2. (2022·乌兰浩特模拟) 如图所示的工件的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·温州模拟) 为研究上半年用水情况，小明把自己家1月至6月份的用水量绘制成折线统计图（如图），根据图中信息，可以判断相邻两个月用水量变化最大的是（　　）

A . 1月至2月 B . 3月至4月 C . 4月至5月 D . 5月至6月

答案解析收藏纠错 + 选题
4. (2020·温州模拟) 在学校“争创美丽班级，争做文明学生”示范班级评比活动中，10位评委给九年级（1）班的评分情况如下表示：

评分（分）

75

80

85

90

评委人数

2

3

4

1

则这10位评委评分的平均数是（　　）

A . 80分 B . 82分 C . 82.5分 D . 85分

答案解析收藏纠错 + 选题
5. (2020·鼓楼模拟) 如图，为了美化校园，学校在一块边角空地建造了一个扇形花圃，扇形圆心角∠AOB＝120°，半径OA为9m，那么花圃的面积为（）

A . 54πm² B . 27πm² C . 18πm² D . 9πm²

答案解析收藏纠错 + 选题
6. (2020·温州模拟) 已知点A（﹣1，y₁）、B（2，y₂）、C（3，y₃）在反比例函数y＝﹣ $\text{[math]}$ 的图象上，则y₁、y₂、y₃的大小关系正确的是（　　）

A . y₂＜y₃＜y₁ B . y₁＜y₃＜y₂ C . y₃＜y₂＜y₁ D . y₃＜y₁＜y₂

答案解析收藏纠错 + 选题
7. (2024九下·贵州模拟) 化简 $\text{[math]}$ 的结果是（　　）

A . x+1 B . x﹣1 C . x D . ﹣x

答案解析收藏纠错 + 选题
8. (2020·温州模拟) 已知关于x、y的二元一次方程组 $\text{[math]}$ 的解满足x+y＜4，则满足条件的k的最大整数为（　　）

A . 3 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题
9. (2020·温州模拟) 如图，▱ABCD的边上一动点P从点C出发沿C﹣D﹣A运动至点A停止，运动的路程计为x，∠ABP与▱ABCD重叠部分面积计为y，其函数关系式如图所示，则▱ABCD中，BC边上的高为（　　）

A . 2 B . 3 C . 4 D . 6

答案解析收藏纠错 + 选题
10. (2020·温州模拟) 如图，将⊙O上的 $\text{[math]}$ 沿弦BC翻折交半径OA于点D，再将 $\text{[math]}$ 沿BD翻折交BC于点E，连结DE．若AB＝10，OD＝1，则线段DE的长为（　　）

A . 5 B . 2 $\text{[math]}$ C . 2 $\text{[math]}$ D . $\text{[math]}$ +1

答案解析收藏纠错 + 选题

二、填空题（共6小题）

11. (2020·温州模拟) 因式分解：m²+6m+9=．

答案解析收藏纠错 + 选题
12. (2020·温州模拟) 为了测试甲、乙两种电子表的走时误差，做了如下统计： $\text{[math]}$ ＝0， $\text{[math]}$ ＝0，S_甲²＝8.8，S_乙²＝4.8，则走时比较稳定的是种电子表．

答案解析收藏纠错 + 选题
13. (2024八下·平谷期末) 函数y= $\text{[math]}$ 中，自变量x的取值范围是．

答案解析收藏纠错 + 选题
14. (2020·温州模拟) 小聪用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每支钢笔5元，则小聪最多可以买几支钢笔？设小聪购买x支钢笔，则可列关于x的一元一次不等式为．

答案解析收藏纠错 + 选题
15. (2024·益阳模拟) 如图，△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，反比例函数y＝ $\text{[math]}$ 在第一象限的图象经过点B，则OA²﹣AB²＝．

答案解析收藏纠错 + 选题
16. (2020·温州模拟) 如图，在Rt△ABC中，∠C＝90°，BC＝2AC，D，E，F分别为BC，AC，AB边上的点，BF＝3AF，∠DFE＝90°，若△BDF与△FEA的面积比为3：2，则△CDE与△DEF的面积比为．

答案解析收藏纠错 + 选题

三、解答题（共8小题）

17. (2020·温州模拟)
1. （1）计算： $\text{[math]}$ ﹣2cos30°+|﹣ $\text{[math]}$ |．
2. （2）化简：a（3﹣a）+（a+1）（a﹣1）．
答案解析收藏纠错 + 选题
18. (2020·温州模拟) 如图，在正方形ABCD中，点E是对角线BD上任意一点，连接AE并延长AE交BC的延长线于点F，交CD于点G．
1. （1）求证：∠DAE＝∠DCE；
2. （2）若∠F＝30°，DG＝2，求CG的长度．
答案解析收藏纠错 + 选题
19. (2020·温州模拟) 图①、图②、图③都是5×5的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，请在所给网格区域（含边界）上按要求画格点三角形．
1. （1）在图①、图②中分别画一个△PAB，使△PAB的面积等于4（所画的两个三角形不全等）．
2. （2）在图③中，画一个△PAB，使tan∠APB＝ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2020·温州模拟) 某学校为了增强学生体质，决定开放以下体育课外活动项目：A．篮球、B．乒乓球、C．跳绳、D．踢毽子．为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图（如图（1），图（2）），请回答下列问题：
1. （1）这次被调查的学生共有人；
2. （2）请你将条形统计图补充完整；
3. （3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
答案解析收藏纠错 + 选题
21. (2020·温州模拟) 如图，在⊙O上依次有A、B、C三点，BO的延长线交⊙O于E， $\text{[math]}$ ，过点C作CD∥AB交BE的延长线于D，AD交⊙O于点F．
1. （1）求证：四边形ABCD是菱形；
2. （2）连接OA、OF，若∠AOF＝3∠FOE且AF＝3，求劣弧 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2020·温州模拟) 名闻遐迩的秦顺明前茶，成本每斤500元，某茶场今年春天试营销，每周的销售量y（斤）与销售单价x（元/斤）满足的关系如下表：

x（元/斤）

550

600

650

680

700

y（斤）

450

400

350

320

300
1. （1）请根据表中的数据猜想并写出y与x之间的函数关系式；
2. （2）若销售每斤茶叶获利不能超过40%，该茶场每周获利w元，试写w与x之间的函数关系式，并求出茶场每周的最大利润．
3. （3）若该茶场每周获利不少于40000元，试确定销售单价x的取值范围．
答案解析收藏纠错 + 选题
23. (2020·温州模拟) 已知二次函数y＝﹣x²+bx+c的图象经过点A（2，0），B（5，0），过点D（0， $\text{[math]}$ ）作y轴的垂线DP交图象于E、F．
1. （1）求b、c的值和抛物线的顶点M的坐标；
2. （2）求证：四边形OAFE是平行四边形；
3. （3）将抛物线向左平移的过程中，抛物线的顶点记为M′，直线DP与抛物线的左交点为E′，连接OM′，OE′，当OE′+OM′的值最小时求直线OE′的解析式．
答案解析收藏纠错 + 选题
24. (2020·温州模拟) 如图，在△ABC中，AB＝7，BC＝4 $\text{[math]}$ ，∠ABC＝45°，射线CD⊥AB于D，点P为射线CD上一动点，以PD为直径的⊙O交PA、PB分别为E、F，设CP＝x．
1. （1）求sin∠ACD的值．
2. （2）在点P的整个运动过程中：
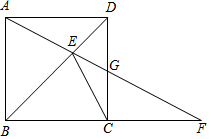
  ①当⊙O与射线CA相切时，求出所有满足条件时x的值；
  
  ②当x为何值时，四边形DEPF为矩形，并求出矩形DEPF的面积．
3. （3）如果将△ADC绕点D顺时针旋转150°，得△A′DC′，若点A′和点C′有且只有一个点在圆内，则x的取值范围是．
答案解析收藏纠错 + 选题