
 B .
B .  C .
C .  D .
D . 
 B .
B . 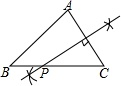 C .
C . 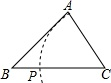 D .
D . 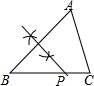
 B .
B .  C .
C . 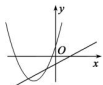 D .
D . 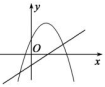

|
学生最喜欢的活动项目的人数统计表 |
||
|
项目 |
学生数(名) |
百分比(%) |
|
袋鼠跳 |
45 |
15 |
|
夹球跑 |
30 |
c |
|
跳大绳 |
75 |
25 |
|
绑腿跑 |
b |
m |
|
拔河赛 |
90 |
30 |

根据图表中提供的信息,解答下列问题:

|
月用水量(吨) |
单价(元/吨) |
|
不大于10吨部分 |
1.5 |
|
大于10吨不大于m吨部分(20≤m≤50) |
2 |
|
大于m吨部分 |
3 |
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成.

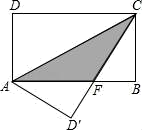
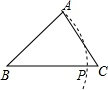
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
①求 的面积(用含
的代数式表示);
②若 的面积为1,当
时,
的最大值为-3,求
的值.