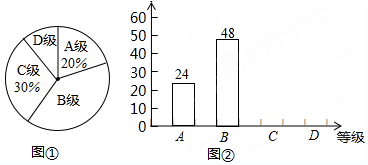
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 


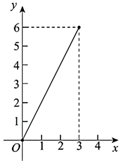
过点B1作l2的垂线交l1于点A2 , 过点A2作x轴的平行线交直线l2于点B2 , 过点B2作l2的垂线交l1于点A3 , 过点A3作x轴的平行线交直线l2于点B3 , ……,过点B1 , B2 , B3 , ……,分别作l1的平行线交A2B2于点C1 , 交A3B3于点C2 , 交A4B4于点C3 , ……,按此规律继续下去,若OA1=1,则点 的坐标为.

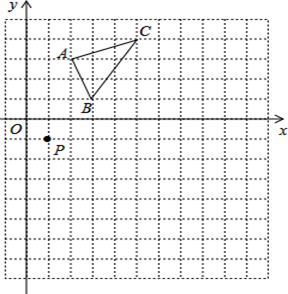
⑴画出△ABC关于x轴对称的△A1B1C1;
⑵以点P(1,﹣1)为位似中心,在如图所示的网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
⑶画出△ABC绕点C逆时针旋转90°的△A′B′C′,并写出线段BC扫过的面积
根据上述信息完成下列问题:


图① 图②
图③
(操作发现)
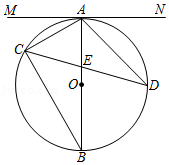
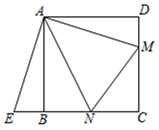
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN .
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE . 易证:△ANM≌△ANE , 从而得DM+BN=MN .
在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是.
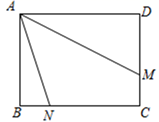
如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN , 已知∠MAN=45°,BN=1,求DM的长.