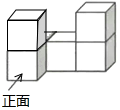
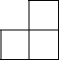
 B .
B . 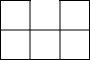 C .
C . 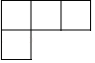 D .
D . 





①在图中补全图形(尺规作图,保留作图痕迹);
②完成下面的证明.
证明:∵OB=OC , DE是线段BC的垂直平分线
∴圆心O在直线DE上().
∵DE⊥BC ,
∴ ().
∴∠BAE=∠CAE(),
∴线段AF为所求△ABC中∠BAC的平分线.

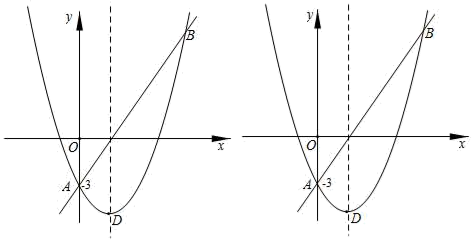
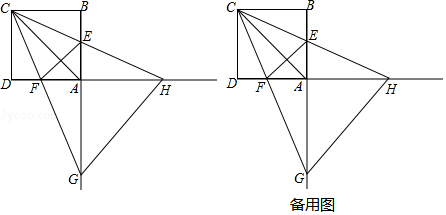
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.