 B .
B .  C .
C .  D .
D . 
 B .
B . 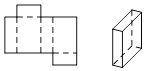 C .
C . 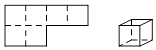 D .
D . 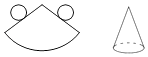
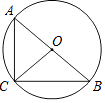
![]()




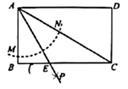
①至少存在一个四边形MNPQ是正方形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④存在无数个四边形MNPQ是平行四边形。所有正确结论的序号是。
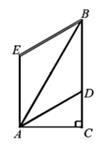

①若点C是线段BD的中点时,则点C的坐标是,b的值是;
②当BC>BD时,直接写出b的取值范围。

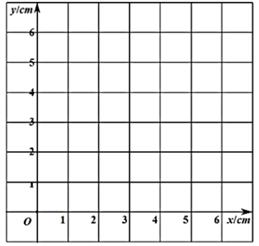
小明根据学习函数的经验,对线段BE,BP,BC的长度之间的关系进行了探究。下面是小明的探究过程。请补充完整:
|
位置1 |
位置2 |
位置3 |
位置4 |
位置5 |
位置6 |
位置7 |
位置8 |
|
|
BC/cm |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
|
BE/cm |
2.10 |
1.32 |
0.53 |
0.00 |
1.32 |
2.10 |
4.37 |
5.6 |
|
BP/cm |
0.52 |
1.07 |
1.63 |
2.00 |
2.92 |
3.48 |
5.09 |
5.97 |
在BE,BP,BC的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数,的长度是常量。

a.甲部门成绩的频数分布直方图如下
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
b.乙部门成绩如下:
乙 40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
| 平均数 | 方差 | 中位数 | |
| 甲 | 79.6 | 36.84 | 78.5 |
| 乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下
| 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
| 出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题
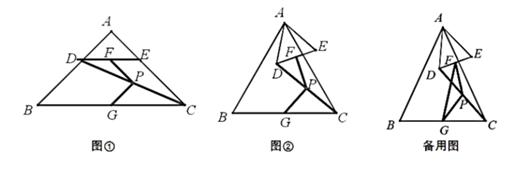


①如图1,在点A(0,1),B(2,0),C(3,4)中,⊙O的称心点是;