吉林省伊通满族自治县2018-2019学年八年级下学期期末考...

更新时间：2024-07-13 浏览次数：243 类型：期末考试

一、选择题

1. (2019八下·北京期末) 函数y= $\text{[math]}$ 的自变量的取值范围是（）

A . x≥2 B . x＜2 C . x＞2 D . x≤2

答案解析收藏纠错 + 选题
2. (2020八下·安阳期末) 下列四组线段中，可以构成直角三角形的是（）

A . 3,4,5 B . $\text{[math]}$ C . 4,5,6 D . 1,1,2

答案解析收藏纠错 + 选题
3. (2019八下·吉林期末) 如图，在▱ABCD中，下列结论不一定正确的是（）

A . ∠1＝∠2 B . ∠1＝∠3 C . AB＝CD D . ∠BAD＝∠BCD

答案解析收藏纠错 + 选题
4. (2023九上·顺德月考) 在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，如果再添加一个条件，即可推出该四边形是正方形，这个条件可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020八上·银川期末) 已知甲、乙、丙三个旅行团的游客人数都相等，且每个旅行团游客的平均年龄都是35岁，这三个旅行团游客年龄的方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，如果你最喜欢带游客年龄相近的旅行团，若在三个旅行团中选一个，则你应选择（）

A . 甲团 B . 乙团 C . 丙团 D . 采取抽签方式，随便选一个

答案解析收藏纠错 + 选题
6. (2019八下·吉林期末) 如图，已知正比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ .下面四个结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2024八上·房山期中) 计算：( $\text{[math]}$ )²=。

答案解析收藏纠错 + 选题
8. (2019八下·吉林期末) 已知有两点 $\text{[math]}$ 、 $\text{[math]}$ 都在一次函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的大小关系是（用“<”连接）

答案解析收藏纠错 + 选题
9. (2019八下·吉林期末) 已知一组数据3、a、4、6的平均数为4，则这组数据的中位数是.

答案解析收藏纠错 + 选题
10. (2020九上·宁德期末) 如图，公路 $\text{[math]}$ 互相垂直，公路 $\text{[math]}$ 的中点 $\text{[math]}$ 与点 $\text{[math]}$ 被湖隔开，若测得 $\text{[math]}$ 的长为2.4km，则 $\text{[math]}$ 两点间的距离为km.

答案解析收藏纠错 + 选题
11. (2023九上·高台月考) 如图，四边形 $\text{[math]}$ 是正方形，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是。

答案解析收藏纠错 + 选题
12. (2024九上·宝安月考) 菱形的两条对角线的长分别为6和8，则这个菱形的周长为.

答案解析收藏纠错 + 选题
13. (2019八下·吉林期末) 如图，在平面直角坐标系中，矩形OABC的顶点A在y轴正半轴上，边AB、OA(AB>OA)的长分别是方程x $\text{[math]}$ −11x+24=0的两个根，D是AB上的一动点(不与A．B重合).AB=8，OA=3.若动点D满足△BOC与AOD相似，则直线OD的解析式为.

答案解析收藏纠错 + 选题
14. (2019八下·吉林期末) 小明用四根长度相同的木条制作了能够活动的菱形学具，他先把活动学具成为图1所示菱形，并测得 $\text{[math]}$ ，接着活动学具成为图2所示正方形，并测得正方形的对角线 $\text{[math]}$ cm，则图1中对角线 $\text{[math]}$ 的长为cm.

答案解析收藏纠错 + 选题

三、综合题

15. (2022八下·仓山期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2019八下·吉林期末) 如图所示，在▱ABCD中，E，F是对角线BD上的两点，且BE=DF，求证：AE=CF

答案解析收藏纠错 + 选题
17. (2019八下·吉林期末) 《九章算术》卷九“勾股”中记载：今有池方一丈，葭生其中央，出水一尺.引葭赴岸，适与岸齐.问霞长几何.
注释：今有正方形水池边长1丈，芦苇生长在中央，长出水面1尺.将芦苇向池岸牵引，恰好与水岸齐，问芦苇的长度（一丈等于10尺）.解决下列问题：
1. （1）示意图中，线段 $\text{[math]}$ 的长为尺，线段 $\text{[math]}$ 的长为尺；
2. （2）求芦苇的长度.
答案解析收藏纠错 + 选题
18. (2021·息县模拟) 小红帮弟弟荡秋千(如图1)，秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示．
1. （1）根据函数的定义，请判断变量h是否为关于t的函数?
2. （2）结合图象回答：
  ①当t=0.7s时，h的值是多少?并说明它的实际意义．
  
  ②秋千摆动第一个来回需多少时间?
答案解析收藏纠错 + 选题
19. (2019八下·吉林期末) 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，在现有网格中，以格点为顶点，分别按下列要求画三角形。
1. （1）在图1中，画一个等腰直角三角形，使它的面积为5；
2. （2）在图2中，画一个三角形，使它的三边长分别为3，2 $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）在图3中，画一个三角形，使它的三边长都是有理数.
答案解析收藏纠错 + 选题
20. (2021八上·河源月考) 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 的表达式为 $\text{[math]}$ ，点A ， B的坐标分别为（1，0），（0，2），直线AB与直线 $\text{[math]}$ 相交于点P ．
1. （1）求直线AB的表达式；
2. （2）求点P的坐标；
3. （3）若直线 $\text{[math]}$ 上存在一点C ，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．
答案解析收藏纠错 + 选题

21. (2019八下·吉林期末) 《中国诗词大会》是央视首档全民参与的诗词节目，节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨，其中的一个比赛环节“飞花令”增加了节目悬念.新学期开学，某班组织了甲、乙两组同学进行了“飞花令”的对抗赛，规定说对一首得1分，比赛中有一方说出9首就结束两个人对抗，得6分以上为合格，得9分以上为优秀，甲、乙两组同学的一次测试成绩如下：

甲组：9，4，6，5，9，6，7，6，8，6，9，5，7，6，9

乙组：4，6，7，6，7，9，7，5，8，7，6，7，9，6，8

（1）请你根据所给的两组数据，绘制统计图（表）.

（2）把下面的表格补充完整.

统计量	平均分（分）	方差（分²）	中位数（分）	合格率	优秀率
甲组		2.56	6	80.0%	26.7%
乙组	6.8	1.76		86.7%	13.3%

（3）根据第（2）题表中数据，你会支持哪一组，并说明理由.

答案解析收藏纠错 + 选题

22. (2023八下·沙坪坝期中) 如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD，AC，BC于点E，O，F，连接CE和AF．
1. （1）求证：四边形AECF为菱形；
2. （2）若AB=4，BC=8，求菱形AECF的周长．
答案解析收藏纠错 + 选题
23. (2019八下·吉林期末) 我们给出如下定义：把对角线互相垂直的四边形叫做“正交四边形”.
如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，四边形 $\text{[math]}$ 就是“正交四边形”.
1. （1）下列四边形，一定是“正交四边形”的是.
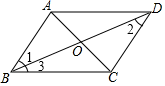
  ①平行四边形②矩形③菱形④正方形
2. （2）如图2，在“正交四边形” $\text{[math]}$ 中，点 $\text{[math]}$ 分别是边 $\text{[math]}$ 的中点，求证：四边形 $\text{[math]}$ 是矩形.
3. （3）小明说：“计算‘正交四边形’的面积可以仿照菱形的方法，面积是对角线之积的一半.”小明的说法正确吗？如果正确，请给出证明；如果不正确，请给出反例.
答案解析收藏纠错 + 选题
24. (2019八下·吉林期末) 甲乙两车分别从A．B两地相向而行，甲车出发1小时后乙车出发，并以各自速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象，其中D点表示甲车到达B地，停止行驶。
1. （1） A、B两地的距离千米；乙车速度是；a=.
2. （2）乙出发多长时间后两车相距330千米?
答案解析收藏纠错 + 选题