辽宁省灯塔市第二初级中学2020年数学中考一模试卷

更新时间：2024-07-31 浏览次数：192 类型：中考模拟

一、选择题

1. (2024七上·北京市期中) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·杭州期中) 下列所给图形是中心对称图形但不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·灯塔模拟) 四个选项中四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体其中有三个几何体的某一种视图都是同一种几何图形，则另外一个几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023七下·江新期中) 下列计算正确的是（　　）

A . 2a²+4a²=6a⁴ B . （a+1）²=a²+1 C . （a²）³=a⁵ D . x⁷÷x⁵=x²

答案解析收藏纠错 + 选题
5. (2019九上·云阳期中) 一元二次方程x²＋2x＋2＝0的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
6. (2020·灯塔模拟) 在一个不透明的袋子中装有5个黑球和3个白球，这些球的大小、质地完全相同，随机地从袋子中摸出4个球，下列事件是必然事件的是（）.

A . 摸出的4个球中至少有一个球是白球 B . 摸出的4个球中至少有一个球是黑球 C . 摸出的4个球中至少有两个球是黑球 D . 摸出的4个球中至少有两个球是白球

答案解析收藏纠错 + 选题
7. (2023九上·建湖月考) 有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2022八下·梅里斯期末) 在“大家跳起来”的乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩，下列说法中错误的是（）

A . 众数是90 B . 中位数是90 C . 平均数是90 D . 极差是15

答案解析收藏纠错 + 选题
9. (2024九上·保定期中) 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A . 菱形 B . 对角线互相垂直的四边形 C . 矩形 D . 对角线相等的四边形

答案解析收藏纠错 + 选题
10. (2020·灯塔模拟) 如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P与点B、C都不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2020·灯塔模拟) 某小区改进了用水设施，在5年内小区的居民累计节水39400吨，将39400用科学记数法表示应为.

答案解析收藏纠错 + 选题
12. (2020·灯塔模拟) 一个盒子里有完全相同的三个小球，球上分别标有数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，随机摸出一个小球（不放回），其数字为 $\text{[math]}$ ，再随机摸出另一个小球其数字记为 $\text{[math]}$ ，则满足关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根的概率是.

答案解析收藏纠错 + 选题
13. (2024七下·江都月考) 已知一个多边形的内角和与外角和的差是1260°，则这个多边形边数是．

答案解析收藏纠错 + 选题
14. (2020·灯塔模拟) 如图，△ABC内接于圆，点D是AC上一点，将∠A沿BD翻折，点A正好落在圆上点E处.若∠C=50°，则∠ABE的度数为.

答案解析收藏纠错 + 选题
15. (2020·灯塔模拟) 关于x的方程 $\text{[math]}$ =1的解是正数，则m的取值范围是 .

答案解析收藏纠错 + 选题
16. (2023·梅州模拟)
如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（结果保留π）.

答案解析收藏纠错 + 选题
17. (2020·灯塔模拟)
如图，将一张边长为6cm的正方形纸片按虚线裁剪后，恰好围成底面是正六边形的棱柱，则这个六棱柱的侧面积为 cm² ．

答案解析收藏纠错 + 选题
18. (2022·普洱模拟) 如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1.先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2016次，点B的落点依次为B₁ ， B₂ ， B₃ ， …，则B₂₀₁₆的坐标为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九上·新泰月考)
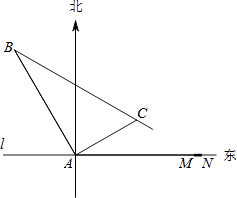
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN（如图），在跑道MN的正西端14.5千米处有一观察站A．某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°，且与点A相距15千米的B处；经过1分钟，又测得该飞机位于点A的北偏东60°，且与点A相距5 $\text{[math]}$ 千米的C处．
1. （1）该飞机航行的速度是多少千米/小时？（结果保留根号）
2. （2）如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN之间？请说明理由．
答案解析收藏纠错 + 选题
20. (2020·灯塔模拟) 九年级七班组织学生参加汉字听写比赛，比赛分为甲、乙、丙三组进行，下面两幅统计图反映了学生参加比赛的报名情况，请你根据图中信息回答下列问题：
1. （1）该班报名参加本次活动的总人数为人.
2. （2）该班报名参加丙组的人数为 ▲ 人，并补全频数分布直方图；
3. （3）比赛后选取男女各2名同学进行培训，若从中选2名参加校赛，试用列表或画树状图的方法，求恰好选中一男一女的概率.
答案解析收藏纠错 + 选题
21. (2020·灯塔模拟) 如图，△ABC是直角三角形，∠ACB＝90°
1. （1）利用尺规作∠ABC 的平分线，交AC 于点O，再以O 为圆心，OC 的长为半径作⊙O(保留作图痕迹，不写作法)；
2. （2）在你所作的图中，①判断AB 与⊙O 的位置关系，并证明你的结论；②若AC＝12，tan∠OBC＝ $\text{[math]}$ ，求⊙O 的半径.
答案解析收藏纠错 + 选题
22. (2020·灯塔模拟) 如图，△ABC中，BC=AC，∠ACB=90°，将△ABC绕着点C顺时针旋转α（0≤α≤90°），得到△EFC，EF与AB、AC相交于点D、H，FC与AB相交于点G.
.
1. （1）求证：△GBC≌△HEC；
2. （2）在旋转过程中，当α是多少度时四边形BCED可以是某种特殊的平行四边形？并说明理由.
答案解析收藏纠错 + 选题
23. (2020·灯塔模拟) 某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：

x（件）

…

5

10

15

20

…

y（元/件）

…

75

70

65

60

…
1. （1）由题意知商品的最低销售单价是元，当销售单价不低于最低销售单价时，y是x的一次函数.求出y与x的函数关系式及x的取值范围；
2. （2）在（1）的条件下，当销售单价为多少元时，所获销售利润最大，最大利润是多少元？
答案解析收藏纠错 + 选题
24. (2020九上·河北期末)
如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．
1. （1）求证：DE⊥AG
2. （2）
  正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．
  ①在旋转过程中，当∠OAG′是直角时，求α的度数；
  ②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．
答案解析收藏纠错 + 选题
25. (2020·灯塔模拟) 如图，二次函数 $\text{[math]}$ 的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴相交于点C（0，﹣4）.
1. （1）求该二次函数的解析；
2. （2）若点P、Q同时从A点出发，以每秒1个单位长度的速度分别沿AB、AC边运动，其中一点到达端点时，另一点也随之停止运动.
  ①当点P运动到B点时，在x轴上是否存在点E，使得以A、E、Q为顶点的三角形为等腰三角形？若存在，请求出E点的坐标；若不存在，请说明理由.
  
  ②当P、Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请直接写出t的值及D点的坐标.
答案解析收藏纠错 + 选题