北京市外国语大学附属中学2020年中考数学模拟试卷

更新时间：2020-06-19 浏览次数：306 类型：中考模拟

一、单选题

1. (2022·宝鸡模拟) 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020·北京模拟) 据环球报报道：中央应对新冠肺炎疫情工作领导小组 3 月 23 日明确，当前以武汉为主战场的全国本土疫情传播基本阻断．过去两个多月，中国为防控疫情做出的巨大努力有目共睹，受到了世卫组织和国际权威公共卫生专家的称赞．其他一些国家也在寻求借鉴中国的经验和防控措施．截止报道前，海外累计确诊病例约 295000 人次．将 295000用科学记数法表示应为（）

A . 2.90×10⁵ B . 0.295×10⁶ C . 2.95×10⁶ D . 2.95×10⁵

答案解析收藏纠错 + 选题
3. (2020·北京模拟) 下列运算一定正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022七下·普陀月考) 如图，将木条 a，b 与 c 钉在一起，∠1 =80°， ∠2 =50°．要使木条 a 与 b 平行，木条 a 旋转的度数至少是（）

A . 10° B . 20° C . 30° D . 50°

答案解析收藏纠错 + 选题
5. (2020八下·沈阳月考) 如果 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 2 C . -2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·北京模拟) 如图，已知⊙O的半径为 6，弦 AB，CD所对的圆心角分别是∠AOB， ∠COD若∠AOB 与∠COD 互补，弦CD=6 ，则弦AB 的长为（）

A . 6 B . 8 C . 3 $\text{[math]}$ D . 6 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·北京模拟) 如图，在菱形 ABCD 中，对角线 AC、BD 相交于点 0，BD=16，tan∠ABD= $\text{[math]}$ 则线段 AB 的长为（）．

A . $\text{[math]}$ B . 10 C . 5 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·北京模拟) 如图，小宇计划在甲、乙、丙、丁四个小区中挑选一个小区租住，附近有东西向的交通主干道a和南北向的交通主干道b ，若他希望租住的小区到主干道a和主干道b的直线距离之和最小，则图中符合他要求的小区是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·宜宾月考) 函数 $\text{[math]}$ 中自变量x的取值范围是．

答案解析收藏纠错 + 选题
10. (2024九上·重庆市开学考) 因式分解： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
11. (2020·北京模拟) 已知点 $\text{[math]}$ 在反比例函数 y = $\text{[math]}$ 的图象上，则 $\text{[math]}$ 与n的大小关系为

答案解析收藏纠错 + 选题
12. (2020·北京模拟) 三角形在正方形网格纸中的位置如图所示，则sinα的值是．

答案解析收藏纠错 + 选题
13. (2023七下·密云期末) 《算法统宗》是中国古代数学名著，作者是明代著名数学家程大位．在其中有这样的记载“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”译文：有100名和尚分100个馒头，正好分完．如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各有几人？设有大和尚x人，小和尚y人，可列方程组为．

答案解析收藏纠错 + 选题
14. (2020·北京模拟) 如图，在正方形 ABCD 中，对角线 AC，BD 相交于点 O，E 是 OB 的中点，连接 AE 并延长交 BC 于点 F，若△BEF 的面积为 2，则△AED 的面积为．

答案解析收藏纠错 + 选题
15. (2020·北京模拟) 我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为 4 的正方形ABCD的边AB在轴x上，AB的中点是坐标原点O固定点A，B，把正方形沿箭头方向推，使点 D落在y 轴正半轴上点 D′处，则点C的对应点C′的坐标为

答案解析收藏纠错 + 选题
16. (2020·北京模拟) 如图，已知∠MON=120°，点A，B分别在OM，ON上，且OA=OB= $\text{[math]}$ ，将射线OM绕点O逆时针旋转得到OM′，旋转角为α（ $\text{[math]}$ 且 $\text{[math]}$ ），作点A关于直线OM′的对称点C，画直线BC交于OM′与点D，连接AC，AD．有下列结论：

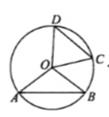
有下列结论：

①∠BDO + ∠ACD = 90°；

②∠ACB 的大小不会随着 $\text{[math]}$ 的变化而变化；

③当 $\text{[math]}$ 时，四边形OADC为正方形；

④ $\text{[math]}$ 面积的最大值为 $\text{[math]}$ ．

其中正确的是．（把你认为正确结论的序号都填上）

答案解析收藏纠错 + 选题

三、解答题

17. (2020·北京模拟) 下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程．
已知：⊙O及⊙O外一点P．

求作：⊙O的一条切线，使这条切线经过点P．

作法：①连接OP，作OP的垂直平分线l，交OP于点A；

②以A为圆心，AO为半径作圆，交⊙O于点M；

③作直线PM，则直线PM即为⊙O的切线．

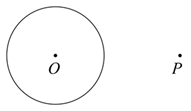
根据小芸设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明：
  证明：连接OM，
  
  由作图可知，A为OP中点，
  
  ∴OP为⊙A直径，
  
  ∴∠＝90°（）（填推理的依据）
  
  即 OM⊥PM．
  
  又∵点M在⊙O上，
  
  ∴PM 是⊙O的切线．（）（填推理的依据）
答案解析收藏纠错 + 选题
18. (2020·北京模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2020·北京模拟) 解不等式组 $\text{[math]}$ ，并将它的解集在数轴上表示，然后写出它的所有整数解

答案解析收藏纠错 + 选题
20. (2020·北京模拟) 已知关于 x 的一元二次方程 $\text{[math]}$ ．
1. （1）求证：方程总有两个实数根；
2. （2）若方程只有一个根是正数，求 m 的取值范围．
答案解析收藏纠错 + 选题
21. (2020·北京模拟) 如图，四边形 ABCD 中，∠C=90°，AD⊥DB，点 E 为 AB 的中点，DE∥BC．
1. （1）求证：BD 平分∠ABC；
2. （2）连接EC，若∠A= $\text{[math]}$ ，DC=3，求EC的长．
答案解析收藏纠错 + 选题
22. (2020·北京模拟) 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD于点E，BF∥OC，连接BC和CF，CF交AB于点G_．
1. （1）求证：∠OCF=∠BCD；
2. （2）若CD=8，tan∠OCF= $\text{[math]}$ ，求⊙O半径的长．
答案解析收藏纠错 + 选题
23. (2020·北京模拟) 在平面直角坐标系xOy中，直线l： $\text{[math]}$ 与x轴交于点A（-2，0），与y轴交于点B．双曲线 $\text{[math]}$ 与直线l交于P，Q两点，其中点P的纵坐标大于点Q的纵坐标．
1. （1）求点B的坐标；
2. （2）当点P的横坐标为2时，求k的值；
3. （3）连接PO，记△POB的面积为S，若 $\text{[math]}$ ，直接写出k的取值范围．
答案解析收藏纠错 + 选题

24. (2020·北京模拟) 如图，Rt△ABC中，∠C=90°，P是CB边上一动点，连接AP，作PQ⊥AP交AB于Q.已知AC=3cm，BC=6cm，设PC的长度为xcm，BQ的长度为ycm.

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.

下面是小青同学的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y的几组对应值；

x/cm	0	0.5	1.0	1.5	2.0	2.5	3	3.5	4	4.5	5	6
y/cm	0	1.56	2.24	2.51	m	2.45	2.24	1.96	1.63	1.26	0.86	0

（说明：补全表格时，相关数据保留一位小数）

m的值约为多少cm；

（2）在平面直角坐标系中，描出以补全后的表格中各组数值所对应的点（x，y），画出该函数的图象；
（3）结合画出的函数图象，解决问题：
①当y>2时，写出对应的x的取值范围；

②若点P不与B，C两点重合，是否存在点P，使得BQ=BP?

答案解析收藏纠错 + 选题

25. (2020·北京模拟) 为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整．

收集数据：

随机抽取甲乙两所学校的20名学生的数学成绩进行分析：

甲	91	89	77	86	71	31	97	93	72	91
	81	92	85	85	95	88	88	90	44	91
乙	84	93	66	69	76	87	77	82	85	88
	90	88	67	88	91	96	68	97	59	88

整理、描述数据：

（1）按如下数据段整理、描述这两组数据
（2）两组数据的平均数、中位数、众数、方差如下表：

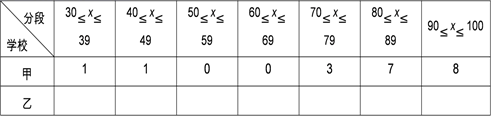
a经统计，表格中m的值是．

得出结论：

b若甲学校有400名初二学生，估计这次考试成绩80分以上人数为．

c可以推断出学校学生的数学水平较高，理由为：①；②．（至少从两个不同的角度说明推断的合理性）

答案解析收藏纠错 + 选题

26. (2020·蠡县模拟) 在平面直角坐标系xOy中，抛物线y＝x²﹣2mx+m²﹣1与y轴交于点C．
1. （1）试用含m的代数式表示抛物线的顶点坐标；
2. （2）将抛物线y＝x²﹣2mx+m²﹣1沿直线y＝﹣1翻折，得到的新抛物线与y轴交于点D．若m＞0，CD＝8，求m的值；
3. （3）已知A（2k，0），B（0，k），在（2）的条件下，当线段AB与抛物线y＝x²﹣2mx+m²﹣1只有一个公共点时，直接写出k的取值范围．
答案解析收藏纠错 + 选题
27. (2020·北京模拟) 如图，在等边 $\text{[math]}$ 中，D为边AC的延长线上一点（ $\text{[math]}$ ），平移线段BC，使点C移动到点D，得到线段ED，M为ED的中点，过点M作ED的垂线，交BC于点F，交AC于点G．
1. （1）依题意补全图形；
2. （2）求证： $\text{[math]}$ ；
3. （3）连接DF并延长交AB于点H，用等式表示线段AH与CG的数量关系，并证明．
答案解析收藏纠错 + 选题
28. (2020·北京模拟) 已知边长为2a的正方形ABCD，对角线AC、BD交于点Q，对于平面内的点P与正方形ABCD，给出如下定义：如果 $\text{[math]}$ ，则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中，若A（﹣1，1），B（﹣1，﹣1），C（1，﹣1），D（1，1）.
1. （1）在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，正方形ABCD的“关联点”有；
2. （2）已知点E的横坐标是m，若点E在直线 $\text{[math]}$ 上，并且E是正方形ABCD的“关联点”，求m的取值范围；
3. （3）若将正方形ABCD沿x轴平移，设该正方形对角线交点Q的横坐标是n，直线 $\text{[math]}$ 与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”，求n的取值范围.
答案解析收藏纠错 + 选题