 B .
B .  C .
C .  D .
D . 
| 最高气温(℃) | 17 | 18 | 20 | 21 | 22 |
| 天数 | 1 | 3 | 2 | 5 | 4 |
则这半月最高气温的众数、中位数分别是( )



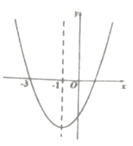
①2a+b=0;
②方程ax2+bx+c=0(a#0)有两个实数根,分别为x1=-3,x2=1;
③4a-2b+c<0;
④一次函数y= x+b的图象不经过第三象限。
其中正确的个数为( )



|
组 别 |
分数分组 |
人数(频数) |
频率 |
|
A |
50≤x<60 |
a |
0.04 |
|
B |
60≤x<70 |
9 |
0.09 |
|
C |
70≤x<80 |
22 |
0.22 |
|
D |
80<x<90 |
b |
n |
|
E |
90≤x<100 |
28 |
0.28 |
|
合计 |
c |
1 |

(注:本次竞赛满分100分,学生得分最低分50分,并且没有满分)
(参考数据:sin24°≈ ,cos 24°≈
,tan24°≈
,sin37°≈
,cos37°≈
,tan 37°≈
)



|
售价x(元/件) |
50 |
60 |
80 |
|
日销售量y(件) |
100 |
80 |
40 |
|
日销售利润w(元) |
1000 |
1600 |
1600 |
注:日销售利润=日销售量×(售价一进价)
如图,有三根针和套在一根针上的n个金属片,按下列规则移动金属片,

规则1:每次只能移动一个金属片;
规则2:较大的金属片不能放在较小的金属片上面.
则把这n个金属片从1号针移到3号针,最少需要移动多少次?
我们从移动1,2,3,4个金属片入手,探究其中的规律性,进而归纳出移动n个金属片所需的次数。
探究一:
当n=1时,只需要把金属片从1号针移到3号针,用符号(13)表示,共移动了1次。(说明:(13)表示把金属片从1号针移到3号针,以此类推)
探究二:
当n=2时,为了避免将较大的金属片放在较小的金属片上面,移动顺序是(本次移动我们借助2号针作为“中间针”):
(Ⅰ)把第1个金属片从1号针移到2号针;
(Ⅱ)把第2个金属片从1号针移到3号针;
(Ⅲ)把第1个金属片从2号针移到3号针。
用符号表示为:(Ⅰ)(12);(Ⅱ)(13);(Ⅲ)(23),共移动了3次。
探究三:
当n=3时,移动顺序是:
(Ⅰ)把上面两个金属片从1号针移到2号针;
(Ⅱ)把第3个金属片从1号针移到3号针;
(Ⅲ)把上面两个金属片从2号针移到3号针。
当n=4时,移动顺序是:
(Ⅰ)把上面个金属片从1号针移到2号针;
(Ⅱ)把第个金属片从1号针移到3号针;
(Ⅲ)把上面个金属片从2号针移到3号针。
……
根据探究一~四,以此类推,你能发现移动规律并对得出的结论进行归纳猜想吗?请你直接写出猜想结果:若把这n个金属片从1号针移到3号针,最少需要移动次。
接PE、PF。设运动时间为t(s)(0<t<8),解答下列问题:


