浙江省台州市路桥区2020年初中毕业生学业考试适应性试卷数学...

更新时间：2020-07-30 浏览次数：297 类型：中考模拟

一、选择题（本题有10小题，每小题4分，共40分.）

1. (2020七上·绛县期中) $\text{[math]}$ 的相反数是（）

A . 2 B . -2 C . $\text{[math]}$ D . ± $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八上·漳州期末) 计算 $\text{[math]}$ 的结果是（）

A . 6a B . 3a² C . 6a² D . 9a²

答案解析收藏纠错 + 选题
3. (2020·路桥模拟) 如图，由5个相同的正方体组合而成的几何体，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·路桥模拟) 若正多边形的一个外角为36°，则这个正多边形是（）

A . 正八边形 B . 正九边形 C . 正十边形 D . 正十一边形

答案解析收藏纠错 + 选题
5. (2021八下·沧州期末) 在战“疫”诗歌创作大赛中，有7名同学进入了决赛，他们的最终成绩均不同.小弘同学想知道自己能否进入前3名，除要了解自己的成绩外，还要了解这7名同学成绩的（）

A . 中位数 B . 平均数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
6. (2020·路桥模拟) 某公司拟购进A，B两种型号机器人.已知用240万元购买A型机器人和用360万元购买B型机器人的台数相同，且B型机器人的单价比A型机器人多10万元.设A型机器人每台x万元，则所列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·杭州模拟) 如图，BC是⊙O的一条弦，经过点B的切线与CO的延长线交于点A，若∠C=23°，则∠A的度数为（）

A . 38° B . 40° C . 42° D . 44°

答案解析收藏纠错 + 选题
8. (2020·路桥模拟) 如图，在矩形ABCD中，将△ABE沿着BE翻折，使点A落在BC边上的点F处，再将△DEG沿着EG翻折，使点D落在EF边上的点H处. 若点A，H，C在同一直线上，AB=1，则AD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·路桥模拟) 甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠.乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售.活动期间，某顾客的草莓采摘量为x kg，若在甲园采摘需总费用y₁元，若在乙园采摘需总费用y₂元. y₁ ， y₂与x之间的函数图象如图所示，则下列说法中错误的是（）

A . 甲园的门票费用是60元 B . 草莓优惠前的销售价格是40元/kg C . 乙园超过5 kg后，超过的部分价格优惠是打五折 D . 若顾客采摘12 kg草莓，那么到甲园或乙园的总费用相同

答案解析收藏纠错 + 选题
10. (2020·路桥模拟) 如图，Rt△ABC中，∠C=90°，BC=6，DE是△ABC的中位线，点D在AB上，把点B绕点D按顺时针方向旋转α（0°<α<180°）角得到点F，连接AF，BF. 下列结论：①△ABF是直角三角形；②若△ABF和△ABC全等，则α=2∠BAC或2∠ABC；③若α=90°，连接EF，则S△DEF=4.5；其中正确的结论是（）

A . ① ② B . ① ③ C . ① ② ③ D . ② ③

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题5分，共30分）

11. (2020·路桥模拟) 二次根式 $\text{[math]}$ 中，a的取值范围是.

答案解析收藏纠错 + 选题
12. (2020·路桥模拟) 已知点A(2，-3)和B(-1，m)均在双曲线 $\text{[math]}$ (k为常数，且k≠0)上，则m=.

答案解析收藏纠错 + 选题
13. (2020·路桥模拟) 在一个不透明的袋子中有三张完全相同的卡片，分别编号为1，2，3.若从中随机取出两张卡片，则卡片上编号之和为偶数的概率是 .

答案解析收藏纠错 + 选题
14. (2020·路桥模拟) 如图，已知△ABC中，AB=AC，∠A=36°，分别以点A，C为圆心，大于 $\text{[math]}$ AC的长度为半径画弧，两弧相交于点P，Q，直线PQ与AB交于点M，若BC=a，MB=b，则AC=.

答案解析收藏纠错 + 选题
15. (2020·路桥模拟) 定义：有一组邻边相等的凸四边形叫做等邻边四边形.如图，在Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线 $\text{[math]}$ 的方向平移，得到△ $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，若四边形 $\text{[math]}$ 是等邻边四边形，则平移距离 $\text{[math]}$ 的长度是.

答案解析收藏纠错 + 选题
16. (2020·路桥模拟) 如图，在正方形ABCD中，AB=6，点E在AB边上，CE与对角线BD交于点F，连接AF，若AE=2，则sin∠AFE的值是.

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，其中第17-20题每题8分，第21题10分，第22-23 题每题12分，第24题14分，共80分）

17. (2020·路桥模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2020·路桥模拟) 解方程组
$\text{[math]}$

答案解析收藏纠错 + 选题
19. (2020·路桥模拟) 等腰三角形的屋顶，是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中，AB=AC，测得BC=20米，∠C=41°，求顶点A到BC边的距离是多少米？（结果精确到0.1米.参考数据：sin41°≈0.656，cos41°≈0.755，tan41°≈0.869.）

答案解析收藏纠错 + 选题

20. (2020·路桥模拟) 如图，“漏壶”是一种古代计时器.在它内部盛一定量的水，水从壶下的小孔漏出.壶内壁有刻度，人们根据壶中水面的位置计算时间.用x（小时）表示漏水时间，y（厘米）表示壶底到水面的高度，某次计时过程中，记录到部分数据如下表：

漏水时间x（小时）	…	3	4	5	6	…
壶底到水面高度y（厘米）	…	9	7	5	3	…

（1）问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种？求出该函数解析式及自变量x的取值范围；
（2）求刚开始计时时壶底到水面的高度.

答案解析收藏纠错 + 选题

21. (2020·路桥模拟) 为了解阳光社区年龄20~60岁居民对垃圾分类的认识，学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查，并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”，B表示“基本能分类”，C表示“略知一二”，D表示“完全不会”.

请根据图中信息解答下列问题：
1. （1）补全条形统计图并填空：被调查的总人数是人，扇形图中D部分所对应的圆心角的度数为；
2. （2）若该社区中年龄20~60岁的居民约3000人，请根据上述调查结果，估计该社区中C类有多少人?
3. （3）根据统计数据，结合生活实际，请你对社区垃圾分类工作提一条合理的建议.
答案解析收藏纠错 + 选题
22. (2020·路桥模拟) 已知AB是⊙O的直径，C是⊙O上的一点（不与点A，B重合），过点C作AB的垂线交⊙O于点D，垂足为E点.
1. （1）如图1，当AE=4，BE=2时，求CD的长度；
2. （2）如图2，连接AC，BD，点M为BD的中点.求证：ME⊥AC.
答案解析收藏纠错 + 选题
23. (2022·珠海模拟) 已知y关于x的二次函数y=x²-bx+ $\text{[math]}$ b²+b-5的图象与x轴有两个公共点.
1. （1）求b的取值范围；
2. （2）若b取满足条件的最大整数值，当m≤x≤ $\text{[math]}$ 时，函数y的取值范围是n≤y≤6-2m，求m，n的值；
3. （3）若在自变量x的值满足b≤x≤b+3的情况下，对应函数y的最小值为 $\text{[math]}$ ，求此时二次函数的解析式.
答案解析收藏纠错 + 选题
24. (2020·路桥模拟) 已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC.
1. （1）如图1，当BM=1时，求PC的长；
2. （2）如图2，设AM与BD交于点E，当∠PCM=45°时，求证： $\text{[math]}$ = $\text{[math]}$ ；
3. （3）如图3，取PC的中点Q，连接MQ，AQ.
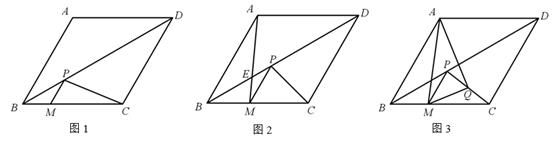
  ①请探究AQ和MQ之间的数量关系，并写出探究过程；
  
  ②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由.
答案解析收藏纠错 + 选题