北京市海淀区2020年中考数学二模试卷

更新时间：2024-07-13 浏览次数：443 类型：中考模拟

一、单选题

1. (2020·海淀模拟) 下面的四个图形中，是圆柱的侧面展开图的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022八上·沙河口期末) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·海淀模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，通过测量，并计算 $\text{[math]}$ 的面积，所得面积与下列数值最接近的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·重庆市月考) 图中阴影部分是由4个完全相同的正方形拼接而成，若要在①，②，③，④四个区域中的某个区域处添加一个同样的正方形，使它与阴影部分组成的新图形是中心对称图形，则这个正方形应该添加在（）

A . 区域①处 B . 区域②处 C . 区域③处 D . 区域④处

答案解析收藏纠错 + 选题
5. (2021九下·乳山期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 70° B . 60° C . 50° D . 40°

答案解析收藏纠错 + 选题
6. (2024九下·临沭模拟) 如果 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2020九上·河东期末) 如图， $\text{[math]}$ 的半径等于4，如果弦 $\text{[math]}$ 所对的圆心角等于90°，那么圆心O到弦 $\text{[math]}$ 的距离为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·北京市模拟) 在平面直角坐标系 $\text{[math]}$ 中，对于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则称点P为“同号点”．下列函数的图象中不存在“同号点”的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2023七上·光山月考) 单项式 $\text{[math]}$ 的系数是.

答案解析收藏纠错 + 选题
10. (2020·海淀模拟) 如图，点A ， B ， C在 $\text{[math]}$ 上，点D在 $\text{[math]}$ 内，则 $\text{[math]}$ $\text{[math]}$ ．（填“>”，“=”或“<”）

答案解析收藏纠错 + 选题

11. (2024九下·海淀模拟) 下表记录了一名篮球运动员在罚球线上投篮的结果：

投篮次数n	48	82	124	176	230	287	328
投中次数m	33	59	83	118	159	195	223
投中频率 $\text{[math]}$	0.69	0.72	0.67	0.67	0.69	0.68	0.68

根据上表，这名篮球运动员投篮一次，投中的概率约为．（结果精确到0.01）

答案解析收藏纠错 + 选题

12. (2020·海淀模拟) 函数 $\text{[math]}$ 的图象上有两点 $\text{[math]}$ ，若 $\text{[math]}$ ，写出一个正确的k的值：．

答案解析收藏纠错 + 选题
13. (2022八下·普宁期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点B作 $\text{[math]}$ ，交 $\text{[math]}$ 于点D ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
14. (2020·海淀模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ，将 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，得到 $\text{[math]}$ ，则点C的对应点 $\text{[math]}$ 的坐标为；再将 $\text{[math]}$ 向上平移一个单位长度，得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
15. (2020·海淀模拟) 小华和小明周末到北京三山五园绿道骑行．他们按设计好的同一条线路同时出发，小华每小时骑行 $\text{[math]}$ ，小明每小时骑行 $\text{[math]}$ ，他们完成全部行程所用的时间，小明比小华多半小时．设他们这次骑行线路长为 $\text{[math]}$ ，依题意，可列方程为．

答案解析收藏纠错 + 选题
16. (2020·海淀模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，有五个点 $\text{[math]}$ ，将二次函数 $\text{[math]}$ 的图象记为W ．下列的判断中
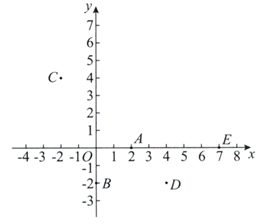
①点A一定不在W上；

②点B ， C ， D可以同时在W上；

③点C ， E不可能同时在W上．

所有正确结论的序号是．

答案解析收藏纠错 + 选题

三、解答题

17. (2020·海淀模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2020·海淀模拟) 解不等式 $\text{[math]}$ ，并在数轴上表示出它的解集．

答案解析收藏纠错 + 选题
19. (2020·海淀模拟) 下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程．
已知：直线l及直线l外一点P ．

求作：直线 $\text{[math]}$ ，使得 $\text{[math]}$ ．

作法：如图，

①在直线l外取一点A ，作射线 $\text{[math]}$ 与直线l交于点B ，

②以A为圆心， $\text{[math]}$ 为半径画弧与直线l交于点C ，连接 $\text{[math]}$ ，

③以A为圆心， $\text{[math]}$ 为半径画弧与线段 $\text{[math]}$ 交于点 $\text{[math]}$ ，

则直线 $\text{[math]}$ 即为所求．

根据小王设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明．
  证明：∵ $\text{[math]}$ ，
  
  ∴ $\text{[math]}$ ，（     ▲    ）（填推理的依据）．
  
  ∵ $\text{[math]}$      ▲    ，
  
  ∴ $\text{[math]}$ ．
  
  ∵ $\text{[math]}$ ，
  
  ∴ $\text{[math]}$ ．
  
  ∴ $\text{[math]}$ （     ▲    ）（填推理的依据）．
  
  即 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2021九上·新丰期中) 已知关于x的一元二次方程 $\text{[math]}$ ．
1. （1）如果此方程有两个相等的实数根，求n的值；
2. （2）如果此方程有一个实数根为0，求另外一个实数根．
答案解析收藏纠错 + 选题
21. (2020·海淀模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，D为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ ，过点C作 $\text{[math]}$ 与 $\text{[math]}$ 相交于点G ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2020·海淀模拟) 坚持节约资源和保护环境是我国的基本国策，国家要求加强生活垃圾分类回收与再生资源回收有效衔接，提高全社会资源产出率，构建全社会的资源循环利用体系．
图1反映了2014—2019年我国生活垃圾清运量的情况．

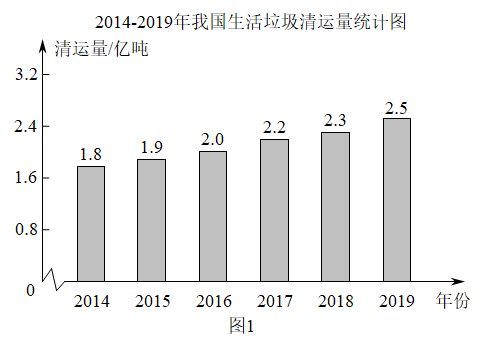
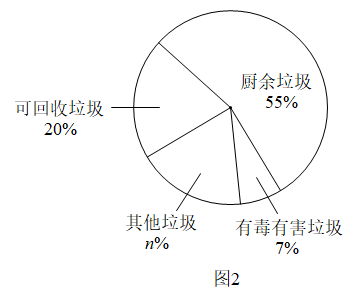
图2反映了2019年我国G市生活垃圾分类的情况．

根据以上材料回答下列问题：
1. （1）图2中，n的值为；
2. （2） 2014—2019年，我国生活垃圾清运量的中位数是；
3. （3）据统计，2019年G市清运的生活垃圾中可回收垃圾约为0.02亿吨，所创造的经济总价值约为40亿元．若2019年我国生活垃圾清运量中，可回收垃圾的占比与G市的占比相同，根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少．
答案解析收藏纠错 + 选题
23. (2020·海淀模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，C为 $\text{[math]}$ 上一点， $\text{[math]}$ 于点E ， $\text{[math]}$ 的切线 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点D ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ．求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2020·海淀模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，函数 $\text{[math]}$ 的图象与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ．M是函数 $\text{[math]}$ 图象上一点，过M作x轴的平行线交直线 $\text{[math]}$ 于点N ．
1. （1）求k和p的值；
2. （2）设点M的横坐标为m ．
  ①求点N的坐标；（用含m的代数式表示）
  
  ②若 $\text{[math]}$ 的面积大于 $\text{[math]}$ ，结合图象直接写出m的取值范围．
答案解析收藏纠错 + 选题
25. (2020·海淀模拟) 如图1，在四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 平分 $\text{[math]}$ ．为了研究图中线段之间的数量关系，设 $\text{[math]}$ ．
1. （1）由题意可得 $\text{[math]}$ ，（在括号内填入图1中相应的线段）y关于x的函数表达式为 $\text{[math]}$ ；
2. （2）如图2，在平面直角坐标系 $\text{[math]}$ 中，根据（1）中y关于x的函数表达式描出了其图象上的一部分点，请依据描出的点画出该函数的图象；
3. （3） ①当 $\text{[math]}$ 时，y随x的增大而增大（答（3）结合函数图象，解决问题：
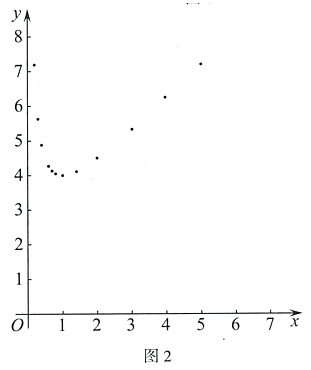
  ①写出该函数的一条性质：；
  
  ②估计 $\text{[math]}$ 的最小值为．（结果精确到0.1）
答案解析收藏纠错 + 选题
26. (2020九上·北京期中) 在平面直角坐标系 $\text{[math]}$ 中，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ ，与y轴交于点B ，将其图象在点A ， B之间的部分（含A ， B两点）记为F ．
1. （1）求点B的坐标及该函数的表达式；
2. （2）若二次函数 $\text{[math]}$ 的图象与F只有一个公共点，结合函数图象，求a的取值范围．
答案解析收藏纠错 + 选题
27. (2020·海淀模拟) 如图1，等边三角形 $\text{[math]}$ 中，D为 $\text{[math]}$ 边上一点，满足 $\text{[math]}$ ，连接 $\text{[math]}$ ，以点A为中心，将射线 $\text{[math]}$ 顺时针旋转60°，与 $\text{[math]}$ 的外角平分线 $\text{[math]}$ 交于点E ．
1. （1）依题意补全图1；
2. （2）求证： $\text{[math]}$ ；
3. （3）若点B关于直线 $\text{[math]}$ 的对称点为F ，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ；
4. （4）若点B关于直线 $\text{[math]}$ 的对称点为F ，连接 $\text{[math]}$ 若 $\text{[math]}$ 成立，直接写出 $\text{[math]}$ 的度数为°．
答案解析收藏纠错 + 选题
28. (2020·海淀模拟) 在平面内，对于给定的 $\text{[math]}$ ，如果存在一个半圆或优弧与 $\text{[math]}$ 的两边相切，且该弧上的所有点都在 $\text{[math]}$ 的内部或边上，则称这样的弧为 $\text{[math]}$ 的内切弧．当内切弧的半径最大时，称该内切弧为 $\text{[math]}$ 的完美内切弧．（注：弧的半径指该弧所在圆的半径）
在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）如图1，在弧 $\text{[math]}$ ，弧 $\text{[math]}$ ，弧 $\text{[math]}$ 中，是 $\text{[math]}$ 的内切弧的是；
2. （2）如图2，若弧G为 $\text{[math]}$ 的内切弧，且弧G与边 $\text{[math]}$ 相切，求弧G的半径的最大值；
3. （3）如图3，动点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
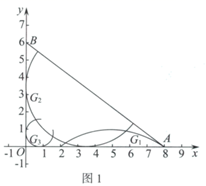
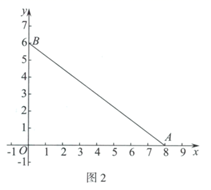
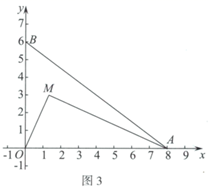
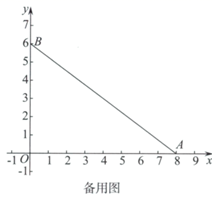
  ①直接写出 $\text{[math]}$ 的完美内切弧的半径的最大值；
  
  ②记①中得到的半径最大时的完美内切弧为弧T ．点P为弧T上的一个动点，过点P作x轴的垂线，分别交x轴和直线 $\text{[math]}$ 于点D ， E ，点F为线段 $\text{[math]}$ 的中点，直接写出线段 $\text{[math]}$ 长度的取值范围．
答案解析收藏纠错 + 选题