2020年高考数学真题试卷（江苏卷）

更新时间：2020-07-13 浏览次数：801 类型：高考真卷

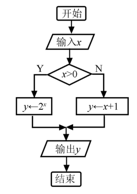
一、填空题：本大题共14小题，每题5分，共计70分．

1. (2020·江苏) 已知集合 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
2. (2020·江苏) 已知i是虚数单位，则复数 $\text{[math]}$ 的实部是.

答案解析收藏纠错 + 选题
3. (2022高一下·青田月考) 已知一组数据 $\text{[math]}$ 的平均数为4，则a的值是.

答案解析收藏纠错 + 选题
4. (2022高一下·汕头期末) 将一颗质地均匀的正方体骰子先后抛掷2次，观察向上的点数，则点数和为5的概率是.

答案解析收藏纠错 + 选题
5. (2021高一下·陈仓期末) 如图是一个算法流程图，若输出y的值为-2，则输入x的值是.

答案解析收藏纠错 + 选题
6. (2020·江苏) 在平面直角坐标系xOy中，若双曲线 $\text{[math]}$ ﹣ $\text{[math]}$ =1(a＞0)的一条渐近线方程为y= $\text{[math]}$ x，则该双曲线的离心率是.

答案解析收藏纠错 + 选题
7. (2020高三上·西藏月考) 已知y=f(x)是奇函数，当x≥0时， $\text{[math]}$ ，则f(-8)的值是.

答案解析收藏纠错 + 选题
8. (2020·江苏) 已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
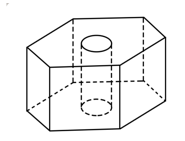
9. (2020·江苏) 如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半轻为0.5 cm，则此六角螺帽毛坯的体积是cm.

答案解析收藏纠错 + 选题
10. (2020·江苏) 将函数y= $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位长度，则平移后的图象中与y轴最近的对称轴的方程是.

答案解析收藏纠错 + 选题
11. (2020·江苏) 设{a_n}是公差为d的等差数列，{b_n}是公比为q的等比数列．已知数列{a_n+b_n}的前n项和 $\text{[math]}$ ，则d+q的值是．

答案解析收藏纠错 + 选题
12. (2021高三上·河西期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是．

答案解析收藏纠错 + 选题
13. (2024高三下·吉首模拟) 在△ABC中， $\text{[math]}$ D在边BC上，延长AD到P，使得AP=9，若 $\text{[math]}$ （m为常数），则CD的长度是．

答案解析收藏纠错 + 选题
14. (2020·江苏) 在平面直角坐标系xOy中，已知 $\text{[math]}$ ，A，B是圆C： $\text{[math]}$ 上的两个动点，满足 $\text{[math]}$ ，则△PAB面积的最大值是．

答案解析收藏纠错 + 选题

二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明，证明过程或演算步骤。

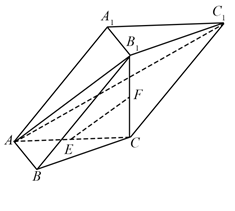
15. (2020·江苏) 在三棱柱ABC-A₁B₁C₁中，AB⊥AC，B₁C⊥平面ABC，E，F分别是AC，B₁C的中点．
1. （1）求证：EF∥平面AB₁C₁；
2. （2）求证：平面AB₁C⊥平面ABB₁ ．
答案解析收藏纠错 + 选题
16. (2021·南通模拟) 在△ABC中，角A，B，C的对边分别为a，b，c，已知 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值；
2. （2）在边BC上取一点D，使得 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
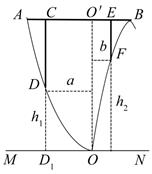
17. (2020·江苏) 某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O在水平线MN上、桥AB与MN平行， $\text{[math]}$ 为铅垂线( $\text{[math]}$ 在AB上).经测量，左侧曲线AO上任一点D到MN的距离 $\text{[math]}$ (米)与D到 $\text{[math]}$ 的距离a(米)之间满足关系式 $\text{[math]}$ ；右侧曲线BO上任一点F到MN的距离 $\text{[math]}$ (米)与F到 $\text{[math]}$ 的距离b(米)之间满足关系式 $\text{[math]}$ .已知点B到 $\text{[math]}$ 的距离为40米.
1. （1）求桥AB的长度；
2. （2）计划在谷底两侧建造平行于 $\text{[math]}$ 的桥墩CD和EF，且CE为80米，其中C，E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价 $\text{[math]}$ (万元)(k>0).问 $\text{[math]}$ 为多少米时，桥墩CD与EF的总造价最低?
答案解析收藏纠错 + 选题
18. (2020·江苏) 在平面直角坐标系xOy中，已知椭圆 $\text{[math]}$ 的左、右焦点分别为F₁ ， F₂ ，点A在椭圆E上且在第一象限内，AF₂⊥F₁F₂ ，直线AF₁与椭圆E相交于另一点B．
1. （1）求△AF₁F₂的周长；
2. （2）在x轴上任取一点P，直线AP与椭圆E的右准线相交于点Q，求 $\text{[math]}$ 的最小值；
3. （3）设点M在椭圆E上，记△OAB与△MAB的面积分别为S₁ ， S₂ ，若S₂=3S₁ ，求点M的坐标．
答案解析收藏纠错 + 选题
19. (2020·江苏) 已知关于x的函数 $\text{[math]}$ 与 $\text{[math]}$ 在区间D上恒有 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求h(x)的表达式；
2. （2）若 $\text{[math]}$ ，求k的取值范围；
3. （3）若 $\text{[math]}$ $\text{[math]}$ 求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2020·江苏) 已知数列 $\text{[math]}$ 的首项a₁=1，前n项和为S_n ．设λ与k是常数，若对一切正整数n，均有 $\text{[math]}$ 成立，则称此数列为“λ–k”数列．
1. （1）若等差数列 $\text{[math]}$ 是“λ–1”数列，求λ的值；
2. （2）若数列 $\text{[math]}$ 是“ $\text{[math]}$ ”数列，且a_n＞0，求数列 $\text{[math]}$ 的通项公式；
3. （3）对于给定的λ，是否存在三个不同的数列 $\text{[math]}$ 为“λ–3”数列，且a_n≥0?若存在，求λ的取值范围；若不存在，说明理由，
答案解析收藏纠错 + 选题

三、【选做题】本题包括21、22、23三小题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．

21. (2020·江苏) [选修4-2：矩阵与变换]
平面上点 $\text{[math]}$ 在矩阵 $\text{[math]}$ 对应的变换作用下得到点 $\text{[math]}$ ．
1. （1）求实数a，b的值；
2. （2）求矩阵M的逆矩阵 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2020·江苏) [选修4-4：坐标系与参数方程]
在极坐标系中，已知点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 在圆 $\text{[math]}$ 上（其中 $\text{[math]}$ ， $\text{[math]}$ ）．
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值
2. （2）求出直线l与圆C的公共点的极坐标．
答案解析收藏纠错 + 选题
23. (2020·江苏) 设 $\text{[math]}$ ，解不等式 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

四、【必做题】第24题、第25题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．

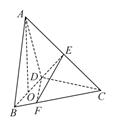
24. (2020·江苏) 在三棱锥A—BCD中，已知CB=CD= $\text{[math]}$ ，BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC的中点．
1. （1）求直线AB与DE所成角的余弦值；
2. （2）若点F在BC上，满足BF= $\text{[math]}$ BC，设二面角F—DE—C的大小为θ，求sinθ的值．
答案解析收藏纠错 + 选题
25. (2020·江苏) 甲口袋中装有2个黑球和1个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为X_n ，恰有2个黑球的概率为p_n ，恰有1个黑球的概率为q_n ．
1. （1）求p₁·q₁和p₂·q₂；
2. （2）求2p_n+q_n与2p_n-1+q_n-1的递推关系式和X_n的数学期望E(X_n)(用n表示) ．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2020年高考数学真题试卷（江苏卷）

副标题：

*注意事项：

2020年高考数学真题试卷（江苏卷）

试题分析

总体分析

题量分析

难度分析

知识点分析