一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
-
4.
(2022·周至模拟)
从一批零件中抽取80个,测量其直径(单位:

),将所得数据分为9组:

,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间

内的个数为( )
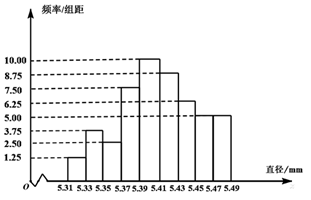
A . 10
B . 18
C . 20
D . 36
-
-
-
7.
(2022高二下·嫩江月考)
设双曲线

的方程为

,过抛物线

的焦点和点

的直线为l.若C的一条渐近线与

平行,另一条渐近线与l垂直,则双曲线C的方程为( )
-
A . ①
B . ①③
C . ②③
D . ①②③
-
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分,
-
-
-
-
13.
(2022·红桥模拟)
已知甲、乙两球落入盒子的概率分别为

和

.假定两球是否落入盒子互不影响,则甲、乙两球都落入盒子的概率为
;甲、乙两球至少有一个落入盒子的概率为
.
-
-
15.
(2022·沧州模拟)
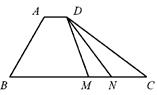
如图,在四边形

中,

,

,且

,则实数

的值为
,若

是线段

上的动点,且

,则

的最小值为
.
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
-
-
17.
(2021高二上·辽宁月考)
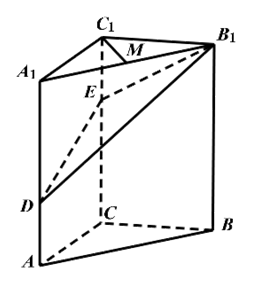
如图,在三棱柱

中,

平面

,

,点

分别在棱

和棱

上,且

为棱

的中点.
(Ⅰ)求证:  ;
;
(Ⅱ)求二面角  的正弦值;
的正弦值;
(Ⅲ)求直线  与平面
与平面  所成角的正弦值.
所成角的正弦值.
-
18.
(2020高二上·重庆月考)
已知椭圆

的一个顶点为

,右焦点为F,且

,其中O为原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点C满足  ,点B在椭圆上(B异于椭圆的顶点),直线
,点B在椭圆上(B异于椭圆的顶点),直线  与以C为圆心的圆相切于点P,且P为线段
与以C为圆心的圆相切于点P,且P为线段  的中点.求直线
的中点.求直线  的方程.
的方程.
-
-
20.
(2020·天津)
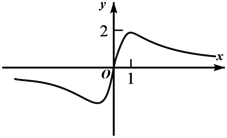
已知函数

,

为

的导函数.
(Ⅰ)当  时,
时,
(i)求曲线  在点
在点  处的切线方程;
处的切线方程;
(ii)求函数  的单调区间和极值;
的单调区间和极值;
(Ⅱ)当  时,求证:对任意的
时,求证:对任意的  ,且
,且  ,有
,有  .
.
 B .
B . 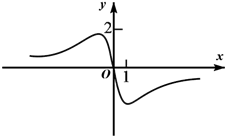 C .
C . 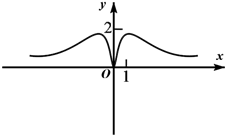 D .
D . 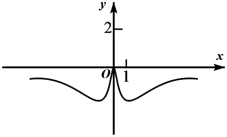
的最小正周期为
;②
是
的最大值;③把函数
的图象上所有点向左平移
个单位长度,可得到函数
的图象.其中所有正确结论的序号是( )

;
的正弦值;
与平面
所成角的正弦值.
,点B在椭圆上(B异于椭圆的顶点),直线
与以C为圆心的圆相切于点P,且P为线段
的中点.求直线
的方程.