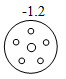
 B .
B .  C .
C . 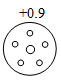 D .
D . 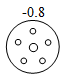
|
尺码 |
S |
M |
L |
XL |
XXL |
XXL |
|
频率 |
0.05 |
0.1 |
0.2 |
0.325 |
0.3 |
0.025 |
则该班学生所穿校服尺码为“L”的人数有个.
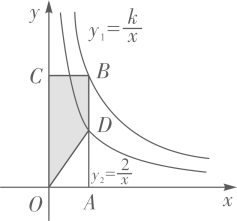
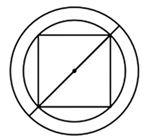
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为尺.(结果用最简根式表示)
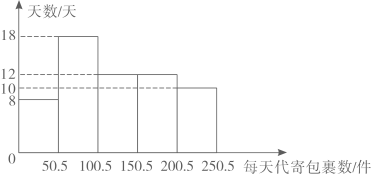
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
|
重量G(单位:千克) |
| | |
| 件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
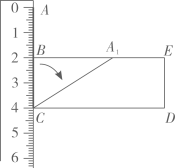
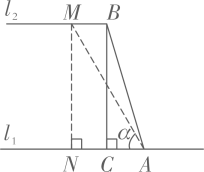
①求证: ;
②把 称为
,
两点间的“ZJ距离”,记为
,求
的值.