
 B .
B .  C .
C . 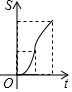 D .
D . 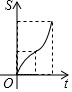
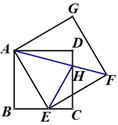

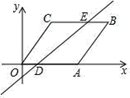
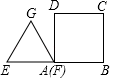
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
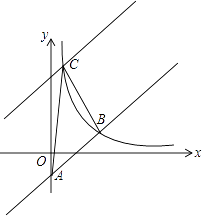
如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.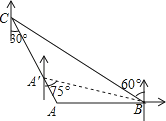
| 销售单价x(元) | 65 | 70 | 75 | 80 | ··· |
| 月销售量y(件) | 475 | 450 | 425 | 400 | ··· |