江苏省泰州医药高新区2020年数学中考二模试卷

更新时间：2020-11-10 浏览次数：303 类型：中考模拟

一、选择题

1. (2020·高新模拟) $\text{[math]}$ 的值等于（）

A . 3 B . －3 C . ±3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·昌平期末) 如果3x=4y（y≠0），那么下列比例式中正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·高新模拟) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·高新模拟) 若点 $\text{[math]}$ ， $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图象上，则代数式 $\text{[math]}$ 的值为（　）

A . 1 B . 2 C . 4 D . 5

答案解析收藏纠错 + 选题
5. (2022·杭州模拟) 某几何体的三视图如图，则该几何体是（）

A . 长方体 B . 圆柱 C . 球 D . 正三棱柱

答案解析收藏纠错 + 选题
6. (2020·石景山模拟) 如图，点A，B，C，D在⊙O上，弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径，②CB＝CE，③AB＝AE中的两个作为题设，余下的一个作为结论组成一个命题，则组成真命题的个数为（　　）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题

7. (2020八上·吉州期末) 4的算术平方根是，9的平方根是，﹣27的立方根是．

答案解析收藏纠错 + 选题
8. (2021八下·顺义期末) 若多边形的内角和是外角和的2倍，则该多边形是边形.

答案解析收藏纠错 + 选题
9. (2020·高新模拟) 人体血液中，红细胞的直径约为0.000 007 7m.用科学记数法表示0.000 007 7m是.

答案解析收藏纠错 + 选题
10. (2023九下·娄星模拟) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
11. (2020·高新模拟) 圆锥的底面半径长为5，将其侧面展开后得到一个半圆，则该半圆的半径长是．

答案解析收藏纠错 + 选题
12. (2020·石景山模拟) 如图，身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时，发现自己在地面上的影子CE长是2米，则路灯的高AB为米.

答案解析收藏纠错 + 选题
13. (2020·平谷模拟) 用一组a，b的值说明命题“如果 $\text{[math]}$ ，那么 $\text{[math]}$ ”是错误的，这组值可以是.

答案解析收藏纠错 + 选题
14. (2020·高新模拟) 一张三角形纸片ABC，其中∠C=90?，AC=6，BC=8.小静同学将纸片做两次折叠：第一次使点A落在C处，折痕记为m；然后将纸片展平做第二次折叠，使点A落在B处，折痕记为n.则m，n的大小关系是.

答案解析收藏纠错 + 选题
15. (2020·西城模拟) 如图，在平面直角坐标系xOy中，点A，B，C的坐标分别是（0，4），（4，0），（8，0），⊙M是△ABC的外接圆，则点M的坐标为.

答案解析收藏纠错 + 选题
16. (2020·高新模拟) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两个动点(点 $\text{[math]}$ 靠近点 $\text{[math]}$ )，且 $\text{[math]}$ ， $\text{[math]}$ 是正方形四边上的任意一点.若 $\text{[math]}$ 是等边三角形，则 AE的长为 .

答案解析收藏纠错 + 选题

三、解答题

17. (2020·高新模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）计算(x＋y)²－y(2x＋y).
答案解析收藏纠错 + 选题
18. (2021八上·潮州期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题
19. (2020九上·南京月考) 已知⊙O及⊙O上一点P，过点P作⊙O的切线.
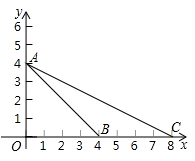
小明设计了如下尺规作法：

①连接OP，以点P为圆心，OP长为半径画弧交⊙O于点A；

②连接OA，延长OA到B，使AB=OA，作直线PB.则直线即为所求作.
1. （1）请证明小明作法的正确性；
2. （2）请你自己再设计一种尺规作图方法（保留痕迹，不要证明）.
答案解析收藏纠错 + 选题
20. (2020·高新模拟) 一只不透明的袋子中装有3个白球、1个红球，这些球除颜色外都相同，搅匀后从中任意摸出2个球.请通过列表或画树状图的方法计算下列事件的概率：
1. （1）摸出的2个球都是白球；
2. （2）摸出的2球是一个红球和一个白球.
答案解析收藏纠错 + 选题

21. (2020·高新模拟) 2020年新冠肺炎疫情发生以来，我市广大在职党员积极参与社区防疫工作，助力社区坚决打赢疫情防控阻击战.其中，A社区有500名在职党员，为了解本社区2月—3月期间在职党员参加应急执勤的情况，A社区针对执勤的次数随机抽取50名在职党员进行调查，并对数据进行了整理、描述和分析，下面给出了部分信息.

次数x/次	频数	频率
0 ≤x< 10	8	0.16
10≤x< 20	10	0.20
20≤x< 30	16	b
30≤x< 40	a	0.24
x≥ 40	4	0.08

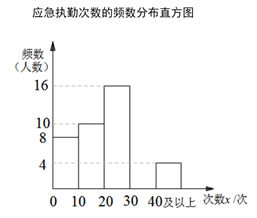
其中，应急执勤次数在20≤x< 30这一组的数据是：

20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29

请根据所给信息，解答下列问题：

（1） $\text{[math]}$ =， $\text{[math]}$ =；
（2）请补全频数分布直方图；
（3）随机抽取的50名在职党员参加应急执勤次数的中位数是；
（4）请估计2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有__人.

答案解析收藏纠错 + 选题

22. (2020·高新模拟) 某市水果批发欲将A市的一批水果运往本市销售，有火车和汽车两种运输方式，运输过程中的损耗均为200元/时，其它主要参考数据如下：

运输工具	途中平均速度（千米/时）	运费（元/千米）	装卸费用（元）
火车	100	15	2000
汽车	80	20	900

（1）如果汽车的总支出费用比火车费用多1100元，你知道本市与A市之间的路程是多少千米吗？请你列方程解答.（总支出包含损耗、运费和装卸费用）
（2）如果A市与B市之间的距离为S千米，你若是A市水果批发部门的经理，要想将这种水果运往B市销售，试分析以上两种运输工具中选择哪种运输方式比较合算呢？

答案解析收藏纠错 + 选题

23. (2020·高新模拟) 如图，大楼AN上悬挂一条幅AB，小颖在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向大楼方向继续行走10米来到C处，测得条幅的底部B的仰角为48°，此时小颖距大楼底端N处20米.已知坡面DE=20米，山坡的坡度i= $\text{[math]}$ ，且D、M、E、C、N、B、A在同一平面内，M、E、C、N在同一条直线上.

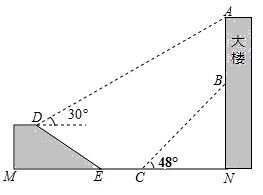
（参考数据：sin48°≈ $\text{[math]}$ ，tan48°≈ $\text{[math]}$ ）
1. （1）求BN的长度；
2. （2）求条幅AB的长度（结果保留根号）.
答案解析收藏纠错 + 选题
24. (2020·石景山模拟) 如图，直线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）过动点 $\text{[math]}$ 作平行于 $\text{[math]}$ 轴的直线，交函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ .
  ①当 $\text{[math]}$ 时，求线段 $\text{[math]}$ 的长；
  
  ②若 $\text{[math]}$ ，结合函数的图象，直接写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
25. (2020·高新模拟) 如图，在矩形ABCD中，AB=3，BC=4，点E在AD上，BE与AC交于点F.
1. （1）若AC⊥BE，求AE的长；
2. （2）设△DEF和△DCF的面积分别为S₁和S₂_，当AE=m时，求S₁：S₂；
3. （3）当AE的长是多少时，△DCF是等腰三角形？
答案解析收藏纠错 + 选题
26. (2020·高新模拟) 二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ （0，-4）和 $\text{[math]}$ （-2，2）.
1. （1）求 $\text{[math]}$ 的值，并用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ ；
2. （2）求证：此抛物线与 $\text{[math]}$ 轴有两个不同交点；
3. （3）当 $\text{[math]}$ 时，若二次函数满足 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小，求 $\text{[math]}$ 的取值范围；
4. （4）直线 $\text{[math]}$ 上有一点 $\text{[math]}$ （ $\text{[math]}$ ，5），将点 $\text{[math]}$ 向右平移4个单位长度，得到点 $\text{[math]}$ ，若抛物线与线段 $\text{[math]}$ 只有一个公共点，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题