北京市西城区2020年中考数学一模试卷

更新时间：2021-04-22 浏览次数：196 类型：中考模拟

一、单选题

1. (2020·西城模拟) 北京大兴国际机场目前是全球建设规模最大的机场，2019年，9月25日正式通航，预计到2022年机场旅客吞吐量将达到45 000 000人次，将45 000 000用科学记数法表示为（）

A . 45× $\text{[math]}$ B . 4.5× $\text{[math]}$ C . 4.5× $\text{[math]}$ D . 0.45× $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·西城模拟) 如图是某个几个几何体的三视图，该几何体是（）

A . 圆锥 B . 圆柱 C . 长方体 D . 正三棱柱

答案解析收藏纠错 + 选题
3. (2020·西城模拟) 下面的图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·西城模拟) 在数轴上，点A，B表示的数互为相反数，若点A在点B的左侧，且AB=2 $\text{[math]}$ ，则点A，点B表示的数分别是（）

A . - $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ，- $\text{[math]}$ C . 0，2 $\text{[math]}$ D . -2 $\text{[math]}$ ，2 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·北京月考) 如图，AB是⊙O的直径，C，D是⊙O上的两点．若∠CAB= $\text{[math]}$ ，则∠ADC的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·西城模拟) 甲、乙两名运动员10次射击成绩(单位，环)如图所示．甲、乙两名运动员射击成绩平均数记为 $\text{[math]}$ ， $\text{[math]}$ ，射击成绩的方差依次记为S_甲² ， S_乙² ，则下列关系中完全正确的是（）

A . $\text{[math]}$ = $\text{[math]}$ ， S_甲² > $\text{[math]}$ B . $\text{[math]}$ = $\text{[math]}$ ， S_甲² < $\text{[math]}$ C . $\text{[math]}$ > $\text{[math]}$ ， S_甲² > $\text{[math]}$ D . $\text{[math]}$ < $\text{[math]}$ ， S_甲² < $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·西城模拟) 如图，在数学实践活动课上，小明同学打算通过测量树的影长计算树的高度，阳光下他测得长1m的竹竿落在地面上的影长为0.9m，在同一时刻测量树的影长时，他发现树的影子有一部分落在地面上，还有一部分落在墙面上，他测得这棵树落在地面上的影长BD为2.7m，落在墙面上的影长CD为1.0m，则这棵树的高度是（）

A . 6.0m B . 5.0m C . 4.0m D . 3.0m

答案解析收藏纠错 + 选题
8. (2022九下·北京市开学考) 设m是非零实数，给出下列四个命题：①若-1<m<0，则 $\text{[math]}$ <m< $\text{[math]}$ ；②若m>1，则 $\text{[math]}$ < $\text{[math]}$ <m；③若m< $\text{[math]}$ < $\text{[math]}$ ，则m<0；④ $\text{[math]}$ <m< $\text{[math]}$ ，则0<m<1．其中命题成立的序号是（）

A . ①③ B . ①④ C . ②③ D . ③④

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·海淀模拟) 若代数式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是。

答案解析收藏纠错 + 选题
10. (2020·西城模拟) 如果一个多边形的内角和等于它的外角和的2倍，那么这个多边形
是边形．

答案解析收藏纠错 + 选题
11. (2022·门头沟模拟) 已知y是以x为自变量的二次函数，且当x=0时，y的最小值为-1，写出一个满足上述条件的二次函数表达式．

答案解析收藏纠错 + 选题
12. (2020·西城模拟) 如果 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
13. (2020·呼和浩特模拟) 如图，在正方形ABCD中，BE平分∠CBD，EF⊥BD于点F，若DE= $\text{[math]}$ ，则BC的长为．

答案解析收藏纠错 + 选题
14. (2022九下·北京市开学考) 如图，△ABC的顶点A，B，C都在边长为1的正方形网格的格点上，BD⊥AC于点D，则AC的长为，BD的长为．

答案解析收藏纠错 + 选题
15. (2020·西城模拟) 如图，在平面直角坐标系xOy中，点A，B，C的坐标分别是（0，4），（4，0），（8，0），⊙M是△ABC的外接圆，则点M的坐标为.

答案解析收藏纠错 + 选题

16. (2020·西城模拟) 某景区为了解游客人数的变化规律，提高旅游服务质量，收集并整理了某月（30天）接待游客人数（单位：万人）的数据，绘制了下面的统计图和统计表：

每日接待游客人数（单位∶万人)	游玩环境评价
0≤x <5	好
5Kx <10	一般
10≤x <15	拥挤
15<x <20	严重拥挤

根据以上信息，以下四个判断中，正确的是．(填写所有符合题意结论的序号)

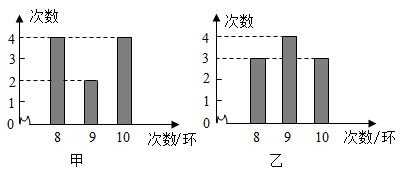
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天；

②该景区这个月每日接待游客人数的中位数在5~10广域网人之间；

③该景区这个月平均每日接待游客人数低于5万人；

④这个月1日至5日的五天中，如果某人曾经随机选择其中的两天到该景区游玩，那么他“这两天游玩环境评价均为好”的可能性为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

17. (2020·西城模拟) 计算： $\text{[math]}$ °．

答案解析收藏纠错 + 选题
18. (2020·西城模拟) 解不等式组 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2020·西城模拟) 关于x的一元二次方程 $\text{[math]}$ 有两个实数根
1. （1）求m的取值范围；
2. （2）写出一个满足条件的m的值，求此时方程的根．
答案解析收藏纠错 + 选题
20. (2021·临清模拟) 如图，在 $\text{[math]}$ ABCD中，对角线AC，BD交于点O，OA=OB，过点B作BE⊥AC于点E．
1. （1）求证： $\text{[math]}$ ABCD是矩形；
2. （2）若AD= $\text{[math]}$ ，cos∠ABE= $\text{[math]}$ ，求AC的长．
答案解析收藏纠错 + 选题
21. (2020·西城模拟) 先阅读下列材料，再解答问题．
尺规作图

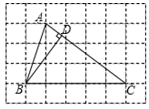
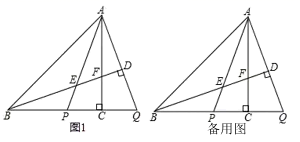
已知：△ABC，D是边AB上一点，如图1，

求作：四边形DBCF，使得四边形DBCF是平行四边形．

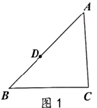
小明的做法如下：

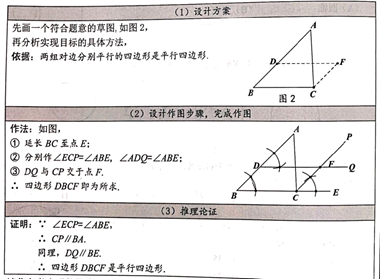
请你参考小明的做法，再设计一一种尺规作图的方法(与小明的方法不同)，使得画出的四边形DBCF是平行四边形，并证明．

答案解析收藏纠错 + 选题

22. (2020·西城模拟) 运用语音识别输入统计可以提高文字输入的速度，为了解A，B两种语音识别输入软件的可读性，小秦同学随机选择了20段话，其中每段话都含有100个字(不计标点符号)，在保持相同条件下，标准普通话来测试两种语音识别输入软件的准确性，整个测试分析过程如下，请补充完整．

收集数据：两种软件每次识别正确的字数记录如下：

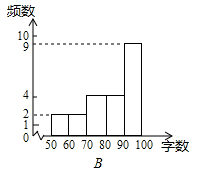
整理，描述数据：根据上面得到的两组样本数据，绘制了分布直方图

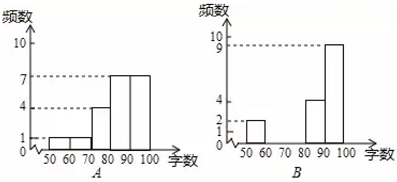
解：统计B组数据得到：60-70的频数为 2，70-80的频数为4，则补全频数分布直方图如图所示：

（1）分析数据：两组样本数据的平均数，众数，中位数，方差如下表所示

	平均数	众数	中位数	方差
A	84.7		84.5	88.91
B	83.7	96		184.01

（2）得出结论：根据以上信息．判断种语音识别输入软件的准确性较好，理由如下．(至少从两个不同的角度说明判断的合理性) ．

答案解析收藏纠错 + 选题

23. (2021九上·北京月考) 如图，四边形OABC中， $\text{[math]}$ ．OA=OC， BA=BC．以O为圆心，以OA为半径作☉O
1. （1）求证：BC是☉O的切线：
2. （2）连接BO并延长交⊙O于点D，延长AO交⊙O于点E，与此的延长线交于点F若 $\text{[math]}$ ．
  ①补全图形；
  
  ②求证：OF=OB．
答案解析收藏纠错 + 选题

24. (2020·西城模拟) 如图，在△ABC中，AB=4cm．BC=5cm，P是 $\text{[math]}$ 上的动点．设A，P两点间的距离为xcm，B，P两点间的距离为 $\text{[math]}$ cm，C，P两点间的距离为 $\text{[math]}$ cm．

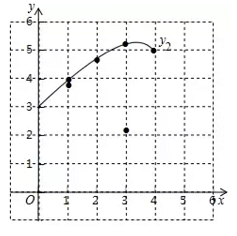
小腾根据学习函数的经验，分别对函数 $\text{[math]}$ ， $\text{[math]}$ 随自变量x的变化而变化的规律进行了探究．

下面是小腾的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了 $\text{[math]}$ ， $\text{[math]}$ 的几组对应值：

x/cm	0	1	2	3	4
$\text{[math]}$ /cm	4.00	3.69		2.13	0
$\text{[math]}$ /cm	3.00	3.91	4.71	5.23	5

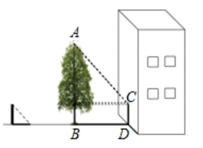
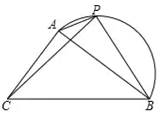
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x， $\text{[math]}$ )，(x， $\text{[math]}$ )，并画出函数 $\text{[math]}$ ， $\text{[math]}$ 的图象：
（3）结合函数图象．
①当△PBC为等腰三角形时，AP的长度约为cm．

②记 $\text{[math]}$ 所在圆的圆心为点O，当直线PC恰好经过点O时，PC的长度约为cm．

答案解析收藏纠错 + 选题

25. (2020·西城模拟) 在平面直角坐标系xOy中，直线L：y=kx+2k(k>0)与x轴交于点A，与y轴交于点B，与函数 $\text{[math]}$ (x>0)的图象的交点P位于第一象限．
1. （1）若点P的坐标为(1，6)，
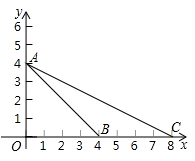
  ①求m的值及点A的坐标；
  
  ② $\text{[math]}$ = ▲ ；
2. （2）直线h：y=2kx-2与y轴交于点C，与直线L₁交于点Q，若点P的横坐标为1，
  ①写出点P的坐标(用含k的式子表示)；
  
  ②当PQ≤PA时，求m的取值范围．
答案解析收藏纠错 + 选题
26. (2020·西城模拟) 已知抛物线y=ax²+bx+a+2(a≠0)与x轴交于点A(x₁ ， 0)，点B(x₂ ， 0)，(点A在点B的左侧)，抛物线的对称轴为直线x=-1．
1. （1）若点A的坐标为(-3，0)，求抛物线的表达式及点B的坐标；
2. （2） C是第三象限的点，且点C的横坐标为-2，若抛物线恰好经过点C，直接写出x₂的取值范围；
3. （3）抛物线的对称轴与x轴交于点D，点P在抛物线上，且∠DOP=45°，若抛物线上满足条件的点P恰有4个，结合图象，求a的取值范围．
答案解析收藏纠错 + 选题
27. (2020·西城模拟) 如图，在等腰直角△ABC中，∠ACB=90 点P在线段BC上，延长BC至点Q，使得CQ=CP，连接AP，AQ．过点B作BD⊥AQ于点D，交AP于点E，交AC于点F．K是线段AD上的一个动点(与点A，D不重合)，过点K作GN⊥AP于点H，交AB于点G，交AC于点M，交FD的延长线于点N．
1. （1）依题意补全图1；
2. （2）求证：NM=NF；
3. （3）若AM=CP，用等式表示线段AE，GN与BN之间的数量关系，并证明．
答案解析收藏纠错 + 选题
28. (2020·西城模拟) 对于平面直角坐标系xOy中的图形W₁和图形W₂ ．给出如下定义：在图形W₁上存在两点A，B（点A，B可以重合），在图形W₂上存在两点M，N，（点M于点N可以重合）使得AM=2BN，则称图形W₁和图形W₂满足限距关系
1. （1）如图1，点C(1，0)，D(-1，0)，E(0， $\text{[math]}$ )，点P在线段DE上运动(点P可以与点D，E重合)，连接OP，CP．
  ①线段OP的最小值为，最大值为；线段CP的取值范直范围是；
  
  ②在点O，点C中，点与线段DE满足限距关系；
2. （2）如图2，⊙O的半径为1，直线 $\text{[math]}$ (b>0)与x轴、y轴分别交于点F，G．若线段FG与⊙O满足限距关系，求b的取值范围；
3. （3） ⊙O的半径为r(r>0)，点H，K是⊙O上的两个点，分别以H，K为圆心，1为半径作圆得到⊙H和¤K，若对于任意点H，K，⊙H和⊙K都满足限距关系，直接写出r的取值范围．
答案解析收藏纠错 + 选题