四川省成都市成华区2019-2020学年七年级下学期数学期末...

更新时间：2024-07-13 浏览次数：313 类型：期末考试

一、单选题

1. (2024七下·萍乡期中) 如图，在线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中，长度最小的是（）

A . 线段 $\text{[math]}$ B . 线段 $\text{[math]}$ C . 线段 $\text{[math]}$ D . 线段 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020七下·成华期末) 中国的方块字中有些具有对称性．下列美术字是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020七下·成华期末) 某种新型冠状病毒的直径为0.000000053米，将0.000000053用科学记数法表示为（）

A . 53×10^﹣⁸ B . 5.3×10^﹣⁷ C . 5.3×10^﹣⁸ D . 5.3×10^﹣⁹

答案解析收藏纠错 + 选题
4. (2020七下·成华期末) “对顶角相等”，这一事件是（）

A . 必然事件 B . 不确定事件 C . 随机事件 D . 不可能事件

答案解析收藏纠错 + 选题
5. (2024七下·成都期中) 下列长度的三条线段，能组成三角形的是（）

A . 4，5，9 B . 6，7，14 C . 4，6，10 D . 8，8，15

答案解析收藏纠错 + 选题
6. (2020七下·成华期末) 下列运算正确的是（）

A . （a³）²＝a⁶ B . a²•a³＝a⁶ C . （a+b）²＝a²+b² D . a²+a³＝a⁵

答案解析收藏纠错 + 选题
7. (2022八上·余姚期中) 如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）

A . ∠A=∠D B . AB=DC C . ∠ACB=∠DBC D . AC=BD

答案解析收藏纠错 + 选题
8. (2020七下·成华期末) 如图，直线AD∥BC，若∠1＝74°，∠BAC＝56°，则∠2的度数为（）

A . 70° B . 60° C . 50° D . 40°

答案解析收藏纠错 + 选题
9. (2021八上·怀宁期末) 如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF对称，∠CAF=10°，连接 BB′，则∠ABB′的度数是（）

A . 30° B . 35° C . 40° D . 45°

答案解析收藏纠错 + 选题
10. (2020八上·成华期末) 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2020七下·天府新期末) 已知∠1=30°，则∠1的补角的度数为度．

答案解析收藏纠错 + 选题
12. (2024七下·银川期中) 某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为．

答案解析收藏纠错 + 选题
13. (2020七下·成华期末) 若a²+b²=6，a+b=3，则ab的值为．

答案解析收藏纠错 + 选题
14. (2020七下·成华期末) 如图，在 $\text{[math]}$ 中，分别以点A和点C为圆心，大于 $\text{[math]}$ 长为半径画弧，两弧相交于点M、N；作直线MN分别交BC、AC于点D、点E ，若 $\text{[math]}$ ， $\text{[math]}$ 的周长为13cm ，则 $\text{[math]}$ 的周长为.

答案解析收藏纠错 + 选题
15. (2024八下·温州开学考) 若2^x=5，2^y=3，则2^2x⁺^y=．

答案解析收藏纠错 + 选题
16. (2020七下·成华期末) 如图，已知1₁∥l₂ ， ∠C＝90°，∠1＝40°，则∠2的度数是．

答案解析收藏纠错 + 选题
17. (2020七下·成华期末) 如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任选取一个白色的小正方形并涂黑，使图中黑色部分的图形仍然构成一个轴对称图形的概率是．

答案解析收藏纠错 + 选题
18. (2021·宣城模拟) 如图，图1是“杨辉三角”数阵；图2是（a+b）ⁿ的展开式（按b的升幂排列）．若（1+x）⁴⁵的展开式按x的升幂排列得：（1+x）⁴⁵＝a₀+a₁x+a₂x²+…+a₄₅x⁴⁵ ，则a₂＝．

答案解析收藏纠错 + 选题
19. (2021八上·北流期末) 如图，AD，BE在AB的同侧，AD＝2，BE＝2，AB＝4，点C为AB的中点，若∠DCE＝120°，则DE的最大值是．

答案解析收藏纠错 + 选题

三、解答题

20. (2020七下·成华期末) 计算：
1. （1）（﹣1）²⁰²⁰﹣（2020﹣π）⁰+（﹣ $\text{[math]}$ ）^﹣²﹣|﹣2|；
2. （2） [（2x²）³﹣6x³（x³﹣2x²）]÷2x⁴ ．
答案解析收藏纠错 + 选题
21. (2020七下·成华期末)
1. （1）先化简，再求值：（x+1）（x﹣1）+（2x﹣1）²﹣2x（2x﹣1），其中x＝﹣2．
2. （2）先化简，再求值：[（2x﹣y）²+（2x﹣y）（2x+y）]÷4x，其中x＝2，y＝﹣1．
答案解析收藏纠错 + 选题

22. (2023七下·通川期末) 为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（ $\text{[math]}$ 分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：

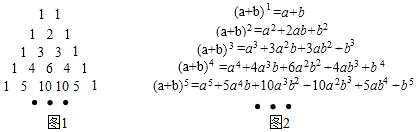
分数段（分）	频数（人）	频率
$\text{[math]}$	$\text{[math]}$	0.1
$\text{[math]}$	18	0.18
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	35	0.35
$\text{[math]}$	12	0.12
合计	100	1

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
（2）将频数分布直方图补充完整；
（3）该校对考试成绩为 $\text{[math]}$ 的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数.

答案解析收藏纠错 + 选题

23. (2020八上·金坛期中) 如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，BD=CE，BE、CD相交于点0；

求证：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
24. (2020七下·成华期末) 某种型号汽车油箱容量为63升，每行驶100千米耗油8升．设一辆加满油的该型号汽车行驶路程为x千米．
1. （1）写出汽车耗油量y（升）与x之间的关系式；
2. （2）写出油箱内剩余油量Q（升）与x之间的关系式；
3. （3）为了有效延长汽车使用寿命，厂家建议汽车油箱内剩余油量为油箱容量的 $\text{[math]}$ 时必须加油．按此建议，问该辆汽车最多行驶多少千米必须加油？
答案解析收藏纠错 + 选题
25. (2020七下·成华期末) 已知：如图，点B在线段AD上， $\text{[math]}$ ABC和 $\text{[math]}$ BDE都是等边三角形，且在AD同侧，连接AE交BC于点G，连接CD交BE于点H，连接GH．
1. （1）求证：AE=CD；
2. （2）求证：AG=CH；
3. （3）求证：GH∥AD．
答案解析收藏纠错 + 选题
26. (2020七下·成华期末) 图1和图2的大正方形都是由一些长方形和小正方形组成的．观察图形，完成下列各题：
1. （1）如图1，求S_大正方形的方法有两种：S_大正方形=(x+y)² ，同时，S_大正方形=S_①+S_②+S_③+S_④=．所以图1可以用来解释等式：；同理图2可以用来解释等式：．
2. （2）已知a+b+c=6，ab+bc+ca=11，利用上面得到的等式，求a²+b²+c²的值．
答案解析收藏纠错 + 选题
27. (2020七下·成华期末) 王老师和小颖住同一小区，小区距离学校2400米．王老师步行去学校，出发10分钟后小颖才骑共享单车出发．小颖途经学校继续骑行若干米到达还车点后，立即跑步返回学校．小颖跑步比王老师步行每分钟快70米．设王老师步行的时间为x（分钟），图1中线段OA和折线B﹣C﹣D分别表示王老师和小颖离开小区的路程y（米）与x（分钟）的关系：图2表示王老师和小颖两人之间的距离S（米）与x（分钟）的关系（不完整）．
1. （1）求王老师步行的速度和小颍出发时王老师离开小区的路程；
2. （2）求小颖骑共享单车的速度和小颖到达还车点时王老师、小颖两人之间的距离；
3. （3）在图2中，画出当25≤x≤30时S关于x的大致图象（要求标注关键数据）．
答案解析收藏纠错 + 选题
28. (2020七下·成华期末)
1. （1）如图1，在 $\text{[math]}$ ABC中，AB=4，AC=6，AD是BC边上的中线，延长AD到点E使DE=AD，连接CE，把AB，AC，2AD集中在 $\text{[math]}$ ACE中，利用三角形三边关系可得AD的取值范围是；
2. （2）如图2，在 $\text{[math]}$ ABC中，AD是BC边上的中线，点E，F分别在AB，AC上，且DE⊥DF，求证：BE+CF＞EF；
3. （3）如图3，在四边形ABCD中，∠A为钝角，∠C为锐角，∠B+∠ADC=180°，DA=DC，点E，F分别在BC，AB上，且∠EDF= $\text{[math]}$ ∠ADC，连接EF，试探索线段AF，EF，CE之间的数量关系，并加以证明．
答案解析收藏纠错 + 选题