北京市西城区三帆中学2019-2020学年八年级上学期数学期...

更新时间：2021-01-12 浏览次数：238 类型：期中考试

一、单选题

1. (2022七上·河口期末) 第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019八上·西城期中) 如图中的两个三角形全等，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·杭州月考) 下列各式中，从左到右的变形是因式分解的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019八上·西城期中) 若 $\text{[math]}$ 是一个完全平方式，则实数 $\text{[math]}$ 的值为（）

A . 36 B . 9 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·烟台期中) 多项式 $\text{[math]}$ 各项的公因式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020八上·北京期中) 下列说法正确的是（）

A . 面积相等的两个三角形是全等三角形 B . 全等三角形是指形状相同的两个三角形 C . 全等三角形的周长和面积分别相等 D . 所有的等腰直角三角形都是全等三角形

答案解析收藏纠错 + 选题
7. (2019八上·西城期中) 已知等腰三角形中有一个角等于 $\text{[math]}$ ，则这个等腰三角形的顶角的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019八上·西城期中) 如图，在纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，则折痕 $\text{[math]}$ 的长为（）

A . 4 B . 3 C . 2 D . 无法确定

答案解析收藏纠错 + 选题
9. (2021八下·泗水期末) 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则 $\text{[math]}$ 点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020八上·休宁期中) 如图，已知 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，如果点 $\text{[math]}$ 在线段 $\text{[math]}$ 上以 $\text{[math]}$ 的速度由点 $\text{[math]}$ 向 $\text{[math]}$ 点运动，同时，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上由点 $\text{[math]}$ 向 $\text{[math]}$ 点以 $\text{[math]}$ 的速度运动.经过（）秒后， $\text{[math]}$ 与 $\text{[math]}$ 全等.

A . 2 B . 3 C . 2或3 D . 无法确定

答案解析收藏纠错 + 选题

二、填空题

11. (2019八上·西城期中) 把多项式 $\text{[math]}$ 分解因式为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
12. (2024八下·北京市期中) 点M（1，2）关于x轴对称的点的坐标为．

答案解析收藏纠错 + 选题
13. (2022八上·长沙期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，要说明 $\text{[math]}$ ，可补充的一个条件为(答案不唯一，写一个即可).

答案解析收藏纠错 + 选题
14. (2023八上·石首期中) 已知 $\text{[math]}$ ，现将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转，使点 $\text{[math]}$ 落在射线 $\text{[math]}$ 上，求作 $\text{[math]}$ .作法：在 $\text{[math]}$ 上截 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧，两弧在射线 $\text{[math]}$ 右侧交于点 $\text{[math]}$ ，则 $\text{[math]}$ 即为所求.此作图确定三角形的依据是：.

答案解析收藏纠错 + 选题
15. (2019八上·西城期中) 已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边上一点，且 $\text{[math]}$ .则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
16. (2019八上·西城期中) $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则中线 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
17. (2019八上·西城期中) 如图， $\text{[math]}$ 平分 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上的一个动点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
18. (2021八上·昌平期末) 已知一张三角形纸片 $\text{[math]}$ 如图甲 $\text{[math]}$ ，其中 $\text{[math]}$ 将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为 $\text{[math]}$ 如图乙 $\text{[math]}$ 再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为 $\text{[math]}$ 如图丙 $\text{[math]}$ 原三角形纸片ABC中， $\text{[math]}$ 的大小为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

19. (2019八上·西城期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2019八上·西城期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2019八上·西城期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
22. (2019八上·西城期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
23. (2019八上·西城期中) 先分解因式，再求值：已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题
24. (2020八上·武安期末) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
25. (2019八上·西城期中) 已知：如图， $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于 $\text{[math]}$ 、 $\text{[math]}$ 两点， $\text{[math]}$ ， $\text{[math]}$ .过 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ . $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的长；
2. （2）求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
26. (2019八上·西城期中) 尺规作图：(保留作图痕迹，不写作法)
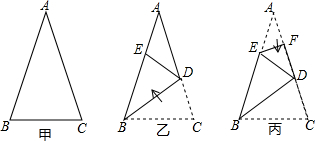
在一节等腰三角形的课上，老师给了一道作图题如下：

已知：线段 $\text{[math]}$ 和线段 $\text{[math]}$ .

求作：等腰 $\text{[math]}$ ，使得底 $\text{[math]}$ ，底边上的高 $\text{[math]}$ .

爱好钻研的小明同学想到作出底边 $\text{[math]}$ 很容易，但是如何在合适的位置尺规作图作出高呢？他经过思考运用等腰三角形的轴对称性得到了顶点 $\text{[math]}$ 所在位置的特征，从而确定了高的画法.

请你继续小明同学的想法并完成尺规作图.

答案解析收藏纠错 + 选题
27. (2019八上·西城期中) 已知：如图， $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 两点分别是边 $\text{[math]}$ 和 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 的交点，连结 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ .求 $\text{[math]}$ 的度数.

证明：∵ $\text{[math]}$ 、 $\text{[math]}$ 两点分别是边 $\text{[math]}$ 和 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 的交点，

∴ $\text{[math]}$     △    ， $\text{[math]}$ .(     △    )

∵ $\text{[math]}$ ，

∴在 $\text{[math]}$ 中， $\text{[math]}$     △    (等量代换)

∴ $\text{[math]}$ 是    △    三角形.

∴ $\text{[math]}$ ，

∵在 $\text{[math]}$ 中， $\text{[math]}$ ，

∴ $\text{[math]}$     △    .

又∵ $\text{[math]}$ 是 $\text{[math]}$ 的外角，

∴ $\text{[math]}$     △    +∠    △    $\text{[math]}$ .

(三角形的一个外角等于与它不相邻的两个内角的和)

∴ $\text{[math]}$     △    .

答案解析收藏纠错 + 选题
28. (2019八上·西城期中) 下列各图中的单位小正方形的边长都等于1，并且都已经填充了一部分阴影，请再对每个图形进行阴影部分的填充，使得图1成为轴对称图形，使得图2成为至少有4条对称轴且阴影部分面积等于3的图形，使得图3成为至少有2条对称轴且面积不超过6的图形.

答案解析收藏纠错 + 选题
29. (2019八上·西城期中) 如图1所示是一个用四根木条钉成的作图工具，其中 $\text{[math]}$ ， $\text{[math]}$ ，两根木条的连接处是可以转动的，几名同学在一起讨论这个工具的用途.
1. （1）小明发现用这个工具可以快速作出角平分线在下面的几种用法中，能作出 $\text{[math]}$ 的平分线的有.(写出所有正确的序号)
  
  ① $\text{[math]}$ 是 $\text{[math]}$ 的平分线； ② $\text{[math]}$ 是 $\text{[math]}$ 的平分线； ③ $\text{[math]}$ 是 $\text{[math]}$ 的平分线
2. （2）对于这个工具的其它用途，小兰发现可以用它作线段的垂直平分线.
  请结合图2补全结论并给出证明.
  
  已知：如图2， $\text{[math]}$ ， $\text{[math]}$ .
  
  求证：垂直平分.
3. （3）对于这个工具的其它用途，小红认为通过多次操作可以用它作平行线.你同意吗？如果同意，请画示意图说明如何操作；如果不同意，请说明理由.
答案解析收藏纠错 + 选题
30. (2019八上·西城期中)
1. （1）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值.
  爱思考的小思想到了一种方法：先用 $\text{[math]}$ 表示 $\text{[math]}$ 得： $\text{[math]}$ ；
  
  再把 $\text{[math]}$ 代入 $\text{[math]}$ 得到： $\text{[math]}$ ；
  
  再利用配方法得到： $\text{[math]}$ ( $\text{[math]}$ ) $\text{[math]}$ +；
  
  根据完全平方式的非负性，就得到了 $\text{[math]}$ 的最小值是.
2. （2）根据小思的方法，请你求出：当 $\text{[math]}$ 时，求出 $\text{[math]}$ 的最小值.
3. （3）但是假如变成 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值的时候小思的方法就不好用了，因此喜欢面对挑战的小喻同学想到了一种叫增量代换法：
  设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
  
  ∵ $\text{[math]}$ ，
  
  ∴ $\text{[math]}$ ，
  
  则 $\text{[math]}$ ，
  
  $\text{[math]}$ ，
  
  $\text{[math]}$ .
  
  故 $\text{[math]}$ 的最小值是 $\text{[math]}$ .
  
  参考小喻的方法，当 $\text{[math]}$ 时，
  
  求出 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题