

 B .
B .  C .
C .  D .
D . 
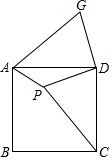
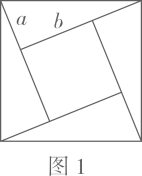
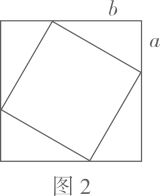
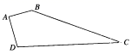
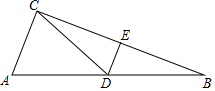

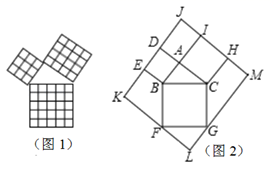
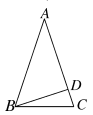
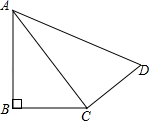

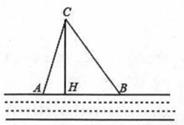
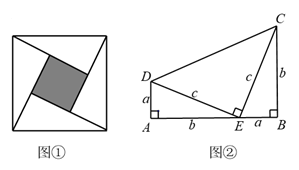
如果直角三角形ABC的两直角边长为3和4,则斜边上的高为.
|
n |
2 |
3 |
4 |
5 |
… |
|
a |
22-1 |
32-1 |
42-1 |
52-1 |
… |
|
b |
4 |
6 |
8 |
10 |
… |
|
c |
22+1 |
32+1 |
42+1 |
52+1 |
… |
a=,b=,c=;