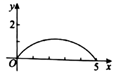
 B .
B . 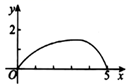 C .
C . 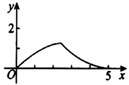 D .
D . 

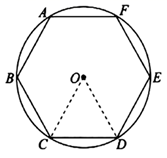
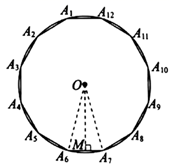
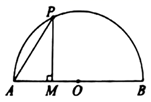
刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割的越细,圆的内接正多边形就越接近圆.设圆的半径为R,圆内接正六边形的周长 ,计算
;圆内接正十二边形的周长
,计算
;请写出圆内接正二十四边形的周长
,计算
.(参考数据:
,
)
| x | … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| | … | | | | | | | | | … |
根据以上信息,关于x的一元二次方程 的两个实数根中,其中的一个实数根约等于(结果保留小数点后一位小数).
小明根据学习二次函数的经验,分析了上面这些函数解析式的特点,研究了它们的图象和性质。下面是小明的分析和研究过程,请补充完整:
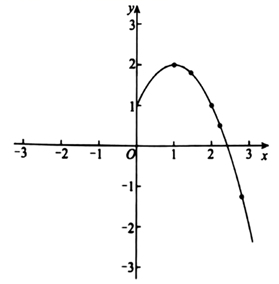
①函数图象关于y轴对称
②有些函数既有最大值,同时也有最小值
③存在某个函数,当 (m为正数)时,y随x的增大而增大,当
时,y随x的增大而减小
④函数图象与x轴公共点的个数只可能是0个或2个或4个
所有符合题意结论的序号是;
①将(1)中的抛物线在A,B两点之间的部分记作 (不含A,B两点),直接写出
上的横整点的坐标;
②抛物线 与直线
交于C,D两点,将抛物线在C,D两点之间的部分记作
(不含C,D两点),若
上恰有两个横整点,结合函数的图象,求m的取值范围.
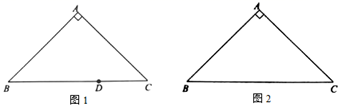
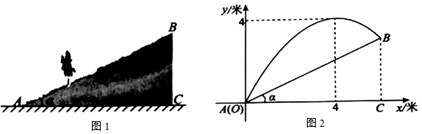
①如图1,点D在边 上,且
,直接写出点D关于
的最大内半圆的半径长;
②如图2,画出 关于
的内半圆,并直接写出它的半径长;