河南省三门峡市渑池县2020-2021学年九年级上学期数学期...

更新时间：2021-10-28 浏览次数：124 类型：期中考试

一、单选题

1. (2020九上·渑池期中) 一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 无实数根 B . 有一个实根 C . 有两个相等的实数根 D . 有两个不相等的实数根

答案解析收藏纠错 + 选题
2. (2021八上·济宁月考) 下列四个图案中，是中心对称图形，但不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九上·广州月考) 设方程 $\text{[math]}$ 的两个根为α，β，那么 $\text{[math]}$ 的值等于（）

A . ﹣3 B . ﹣1 C . 1 D . 3

答案解析收藏纠错 + 选题
4. (2020九上·渑池期中) 疫情期间，某快递公司推出无接触配送服务，第1周接到5万件订单，第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍，若第3周接到订单为7.8万件，设第1周到第2周的订单增长率为 $\text{[math]}$ ，可列得方程为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·渑池期中) 如图，A、B、C三点在 $\text{[math]}$ 上，D是 $\text{[math]}$ 延长线上的一点， $\text{[math]}$ ，那么 $\text{[math]}$ 的度数为（）.

A . 80° B . 70° C . 50° D . 40°

答案解析收藏纠错 + 选题
6. (2020九上·莘县期末) 如图，在⊙O中，直径AB⊥CD，∠A＝26°，则∠D度数是（　　）

A . 26° B . 38° C . 52° D . 64°

答案解析收藏纠错 + 选题
7. (2020九上·渑池期中) 对于二次函数 y = -2(x + 3) $\text{[math]}$ 的图象，下列说法不正确的是（）

A . 开口向下 B . 对称轴是直线 x = -3 C . 顶点坐标为(-3， 0) D . 当 x < -3 时，y 随 x 的增大而减小

答案解析收藏纠错 + 选题
8. (2020九上·渑池期中) 二次函数 $\text{[math]}$ 的图象如图所示，那么一次函数 $\text{[math]}$ 的图象大致是（）.

A . B . C . D .

答案解析收藏纠错 + 选题
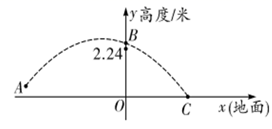
9. (2020九上·渑池期中) 2019年女排世界杯于9月在日本举行，中国女排以十一连胜的骄人成绩卫冕冠军，充分展现了团队协作、顽强拼搏的女排精神．如图是某次比赛中垫球时的动作，若将垫球后排球的运动路线近似的看作拋物线，在同一竖直平面内建立如图所示的直角坐标系，已知运动员垫球时（图中点 $\text{[math]}$ ）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图中点 $\text{[math]}$ ）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图中点 $\text{[math]}$ ）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·渑池期中) 如图，在平面直角坐标系中，将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转45°后得到正方形 $\text{[math]}$ ，依此方式，绕点 $\text{[math]}$ 连续旋转2020次得到正方形 $\text{[math]}$ ，如果点 $\text{[math]}$ 的坐标为（1，0），那么点 $\text{[math]}$ 的坐标为（）

A . (﹣1，1) B . $\text{[math]}$ C . (﹣1，﹣1) D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·渑池期中) 如果一元二次方程 $\text{[math]}$ 经配方后变为 $\text{[math]}$ ，则实数k的值为.

答案解析收藏纠错 + 选题
12. (2020九上·渑池期中) 关于x的方程kx²﹣4x $\text{[math]}$ ＝0有两个实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
13. (2020九上·渑池期中) 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，下列结论：①b²＞4ac，②abc＜0，③2a+b﹣c＞0，④a+b+c＜0.其中正确的是.

答案解析收藏纠错 + 选题
14. (2023·黄冈模拟) 将抛物线 $\text{[math]}$ 向上平移3个单位长度后，经过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
15. (2020九上·渑池期中) 某公司新产品上市30天全部售完，图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，则最大日销售利润是元.

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·渑池期中) 用指定的方法解下列方程：
1. （1） $\text{[math]}$ （配方法）
2. （2） $\text{[math]}$ （公式法）
答案解析收藏纠错 + 选题
17. (2020九上·渑池期中) 筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图 $\text{[math]}$ ，点 $\text{[math]}$ 表示筒车的一个盛水桶．如图 $\text{[math]}$ ，当筒车工作时，盛水桶的运行路径是以轴心 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径的圆，且圆心在水面上方．若圆被水面截得的弦 $\text{[math]}$ 长为 $\text{[math]}$ ，求筒车工作时，盛水桶在水面以下的最大深度．

答案解析收藏纠错 + 选题
18. (2020九上·渑池期中) 如图，等腰直角 $\text{[math]}$ 的直角边与正方形 $\text{[math]}$ 的边长均为 $\text{[math]}$ ，边 $\text{[math]}$ 与边 $\text{[math]}$ 在同一直线上，点A与点M重合，让 $\text{[math]}$ 沿 $\text{[math]}$ 方向以 $\text{[math]}$ 的速度匀速运动，运动到点A与N重合时停止，设运动的时间为t，运动过程中 $\text{[math]}$ 与正方形 $\text{[math]}$ 的重叠部分面积为S，
1. （1）试写出S关于t的函数关系式，并指出自变量t的取值范围.
2. （2）当 $\text{[math]}$ 时，重叠部分的面积是多少？
答案解析收藏纠错 + 选题
19. (2020九上·渑池期中) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足为E.
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2021八下·武义期中) 如图1，有一张长 $\text{[math]}$ 宽 $\text{[math]}$ 的长方形硬纸片，裁去角上 $\text{[math]}$ 个小正方形和 $\text{[math]}$ 个小长方形（图中阴影部分）之后，恰好折成如图2的有盖纸盒.
1. （1）若纸盒的高是 $\text{[math]}$ cm，求纸盒底面长方形的长和宽；
2. （2）若纸盒的底面积是 $\text{[math]}$ ，求纸盒的高.
答案解析收藏纠错 + 选题
21. (2020九上·渑池期中) 有一家苗圃计划种植桃树和柏树，根据市场调查与预测，种植桃树的利润y₁（万元）与投资成本x（万元）满足如图1所示的二次函数y₁＝ax²；种植柏树的利润y₂（万元）与投资成本x（万元）满足如图2所示的正比例函数y₂＝kx ．
1. （1）请分别直接写出利润y₁（万元）与利润y₂（万元）关于投资成本x（万元）的函数关系式；
2. （2）若这家苗圃投资4万元种植桃树，投资6万元种植柏树，则可获得的总利润是多少万元？
3. （3）若这家苗圃种植桃树和柏树投入总成本20万元，且桃树的投资成本不低于2万元，且不高于12万元，则苗圃最少能获得多少总利润？最多可获得多少总利润？
答案解析收藏纠错 + 选题
22. (2020九上·渑池期中) 如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG.
1. （1）如图1，若AD＝2 $\text{[math]}$ 、DE＝2，当 $\text{[math]}$ 时，求AG的长；
2. （2）如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE之间有何等量关系？并利用图2加以证明.
答案解析收藏纠错 + 选题
23. (2020九上·渑池期中) 在平面直角坐标系中，点O为坐标原点，抛物线y=﹣x²+（k﹣1）x+k（k＞0）交x轴的负半轴于点A，交x轴的正半轴于点B，交y轴的正半轴于点C，且AB=4．
1. （1）如图1，求k的值；
2. （2）如图2，点D在第一象限的抛物线上，点E在线段BC上，DE//y轴，若DE= $\text{[math]}$ BE，求点D的坐标；
3. （3）如图3，在（2）的条件下，F为抛物线顶点，点P在第四象限的抛物线上，FP交直线DE于点Q，点G与点D关于y轴对称，若GQ=DP，求点P的坐标．
答案解析收藏纠错 + 选题