

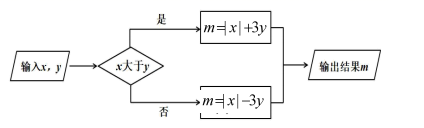
表2:商场促销方案
①所有商品均享受8折优惠.
②所有洗衣机均可享受节能减排补贴,补贴标准为:在折后价的基础t.
再减免13%。
③若同时购买同品牌洗 衣机和烘干机,额外可享受“满两件减400元"
则选择品种的洗衣机和品种的烘干机支付总费用最低,支付总费用最低为元.


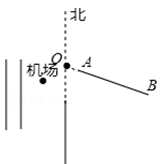
当点 与原点
重合时,用等式表示
与
的关系为;
若三点 的位置如图所示,请在图中标出点
的位置;


小聪是这样思考的:首先通过分析明确射线 在
的外部,画出示意图,如图2所示:然后通过构造平角找到
的补角
,

如图3所示:进而分析要使 与
互补,则需
.

因此,小聪找到了解决问题的方法:反向延长射线 得到射线
,利用量角器画出
的平分线
,这样就得到了
与
互补



根据以上材料,解决下列问题:
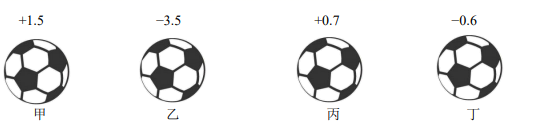
①判断 这三个数中哪些与
“模二相加不变”,并说明理由;